2-Manifold Learning
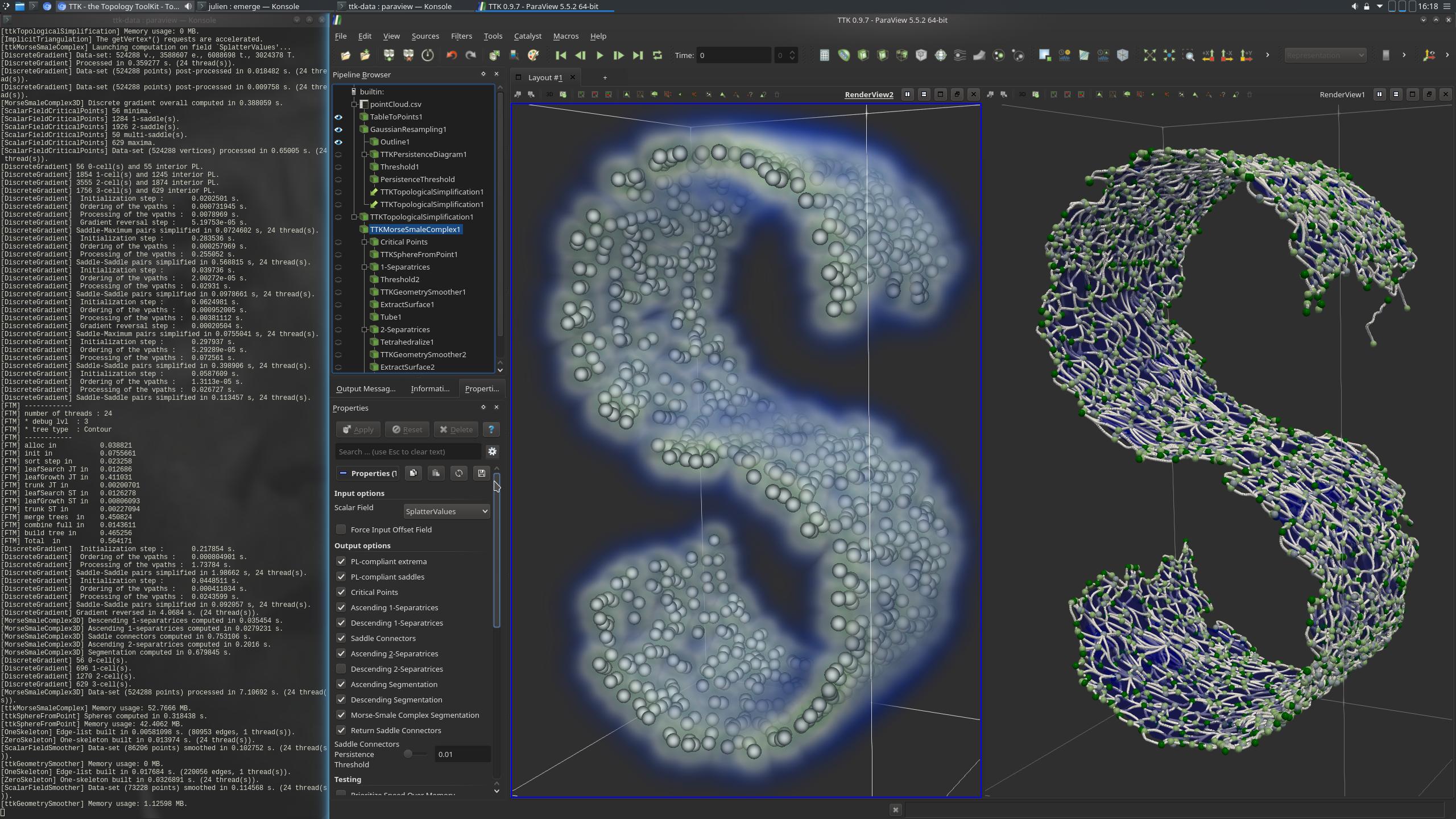
Pipeline description
This example first loads a point cloud from disk.
In a pre-processing, the data is converted to a format understandable by Paraview using the TableToPoints filter. GaussianResampling is applied to the data (left view in the above screenshot). This filter has the effect of injecting input points to a structured data. For each injection, each point will "splat", or distribute values to nearby vertices. The resulting scalar field is a density estimation (with a Gaussian kernel) of the input point cloud.
Then, the PersistenceDiagram is computed and thresholds are applied based on persistence to maintain only the most persistent features. This results in a simplified persistence diagram.
The simplified persistence diagram is then used as a constraint for the TopologicalSimplification of the input scalar data.
This simplified data is then used as the input of the computation of MorseSmaleComplex (right view, above screenshot). This complex is composed of elements of 4 dimensions: dimension 0, which corresponds to the critical points of the Morse-Smale Complex, dimension 1, which corresponds to its edges (in grey in the screenshot) and dimension 2, which corresponds to its surfaces, and dimension 3, which corresponds to pieces of volume that can be extracted from the Segmentation output. The "S" shape made by the point cloud is outlined by the maximal 1 and 2 dimension elements of the Morse-Smale Complex.
ParaView
To reproduce the above screenshot, go to your ttk-data directory and enter the following command:
paraview states/2manifoldLearning.pvsm
Python code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65 | #!/usr/bin/env python
from paraview.simple import *
# create a new 'CSV Reader'
pointCloudcsv = CSVReader(FileName=["pointCloud.csv"])
# create a new 'Table To Points'
tableToPoints1 = TableToPoints(Input=pointCloudcsv)
tableToPoints1.XColumn = "Points:0"
tableToPoints1.YColumn = "Points:1"
tableToPoints1.ZColumn = "Points:2"
# create a new 'Gaussian Resampling'
gaussianResampling1 = GaussianResampling(Input=tableToPoints1)
gaussianResampling1.ResampleField = ["POINTS", "ignore arrays"]
gaussianResampling1.ResamplingGrid = [64, 64, 128]
# create a new 'TTK PersistenceDiagram'
tTKPersistenceDiagram1 = TTKPersistenceDiagram(Input=gaussianResampling1)
tTKPersistenceDiagram1.ScalarField = ["POINTS", "SplatterValues"]
# create a new 'Threshold'
threshold1 = Threshold(Input=tTKPersistenceDiagram1)
threshold1.Scalars = ["CELLS", "PairIdentifier"]
threshold1.ThresholdMethod = "Between"
threshold1.LowerThreshold = -0.1
threshold1.UpperThreshold = 999999999
# create a new 'Threshold'
persistenceThreshold = Threshold(Input=threshold1)
persistenceThreshold.Scalars = ["CELLS", "Persistence"]
persistenceThreshold.ThresholdMethod = "Between"
persistenceThreshold.LowerThreshold = 0.01
persistenceThreshold.UpperThreshold = 999999
# create a new 'TTK TopologicalSimplification'
tTKTopologicalSimplification1 = TTKTopologicalSimplification(
Domain=gaussianResampling1, Constraints=persistenceThreshold
)
tTKTopologicalSimplification1.ScalarField = ["POINTS", "SplatterValues"]
# create a new 'TTK MorseSmaleComplex'
tTKMorseSmaleComplex1 = TTKMorseSmaleComplex(Input=tTKTopologicalSimplification1)
tTKMorseSmaleComplex1.ScalarField = ["POINTS", "SplatterValues"]
tTKMorseSmaleComplex1.Ascending2Separatrices = 1
tTKMorseSmaleComplex1.ReturnSaddleConnectors = 1
tTKMorseSmaleComplex1.SaddleConnectorsPersistenceThreshold = 0.01
tTKMorseSmaleComplex1.ThresholdIsAbsolute = True
# create a new 'Tetrahedralize'
tetrahedralize1 = Tetrahedralize(Input=OutputPort(tTKMorseSmaleComplex1, 2))
# create a new 'TTK GeometrySmoother'
tTKGeometrySmoother2 = TTKGeometrySmoother(Input=tetrahedralize1)
tTKGeometrySmoother2.IterationNumber = 20
tTKGeometrySmoother2.InputMaskField = [None, ""]
# threshold the output surface
threshold5 = Threshold(Input=tTKGeometrySmoother2)
threshold5.Scalars = ['CELLS', 'SeparatrixFunctionMinimum']
threshold5.LowerThreshold = 0.2
threshold5.UpperThreshold = 1
SaveData("OutputSurface.vtu", threshold5)
|
To run the above Python script, go to your ttk-data directory and enter the following command:
pvpython python/2manifoldLearning.py
Outputs
OutputSurface.vtu: surface (or 2 dimensional elements) of the output Morse Smale Complex in VTK file format (right view, above screenshot). You are free to change the vtp file extension to that of any other supported file format (e.g. csv) in the above python script.
C++/Python API
GeometrySmoother
MorseSmaleComplex
PersistenceDiagram
TopologicalSimplification
