Topology ToolKit

Persistent Homology for Dummies

The purpose of this exercise tutorial is threefold:
   ·  Introduce you to the usage of TTK in ParaView and Python;
   ·  Introduce you to persistent homology from a practical point of view;
   ·  Introduce you to the applications of persistent homology to medical data segmentation.

This exercise requires some very mild background in Python.
It should take no more than 2 hours of your time.

1. Downloads

In the following, we will assume that TTK has been installed successfully on your system. If not, please visit our installation page for detailed instructions HERE.
Before starting the exercise, please download the data package HERE.
Move the tarball to a working directory (for instance called ~/ttk) and decompress it by entering the following commands (omit the $ character) in a terminal (this assumes that you downloaded the tarball to the ~/Downloads directory):

$ mkdir ~/ttk
$ mv ~/Downloads/ttk-data-0.9.3.tar.gz ~/ttk/
$ cd ~/ttk
$ tar xvzf ttk-data-0.9.3.tar.gz

You can delete the tarball after decompression by entering the following command:

$ rm ttk-data-0.9.3.tar.gz

2. TTK/ParaView 101

ParaView is the leading application for the interactive analysis and visualization of scientific data. It is open-source (BSD license). It is developed by Kitware, a prominent company in open-source software (CMake, CDash, VTK, ITK, etc.).

ParaView is a graphical user interface to the Visualization ToolKit, a C++ library for data visualization and analysis, also developed in open-source by Kitware.
VTK and ParaView both implement a pipeline model, where the data to analyze and visualize is passed on the input of a (possibly complex) sequence of elementary processing units, called filters. Each filter is implemented by a single C++ class in VTK. In ParaView, users can design advanced processing pipelines by placing manually each filter in their pipelines.
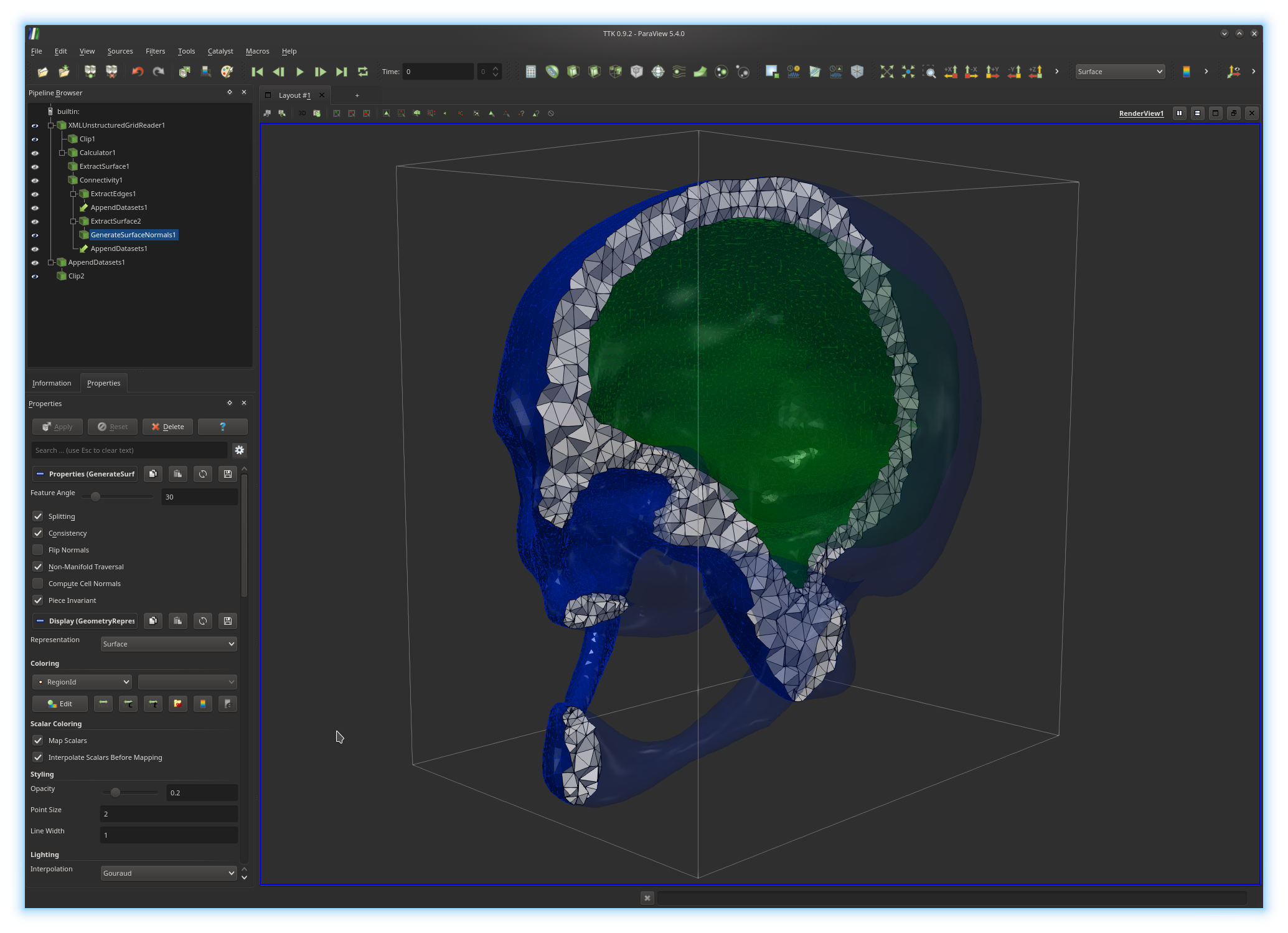
In the above example, the active pipeline (shown in the "Pipeline Browser", upper left panel) can be interpreted as a series of processing instructions and reads similarly to some source code: first, the input PL 3-manifold is clipped (Clip1); second, the boundary of the input PL 3-manifold is extracted (ExtractSurface1), third the connected components of the boundary are isolated and clipped with the same parameters as the rest of the volume (Clip2).

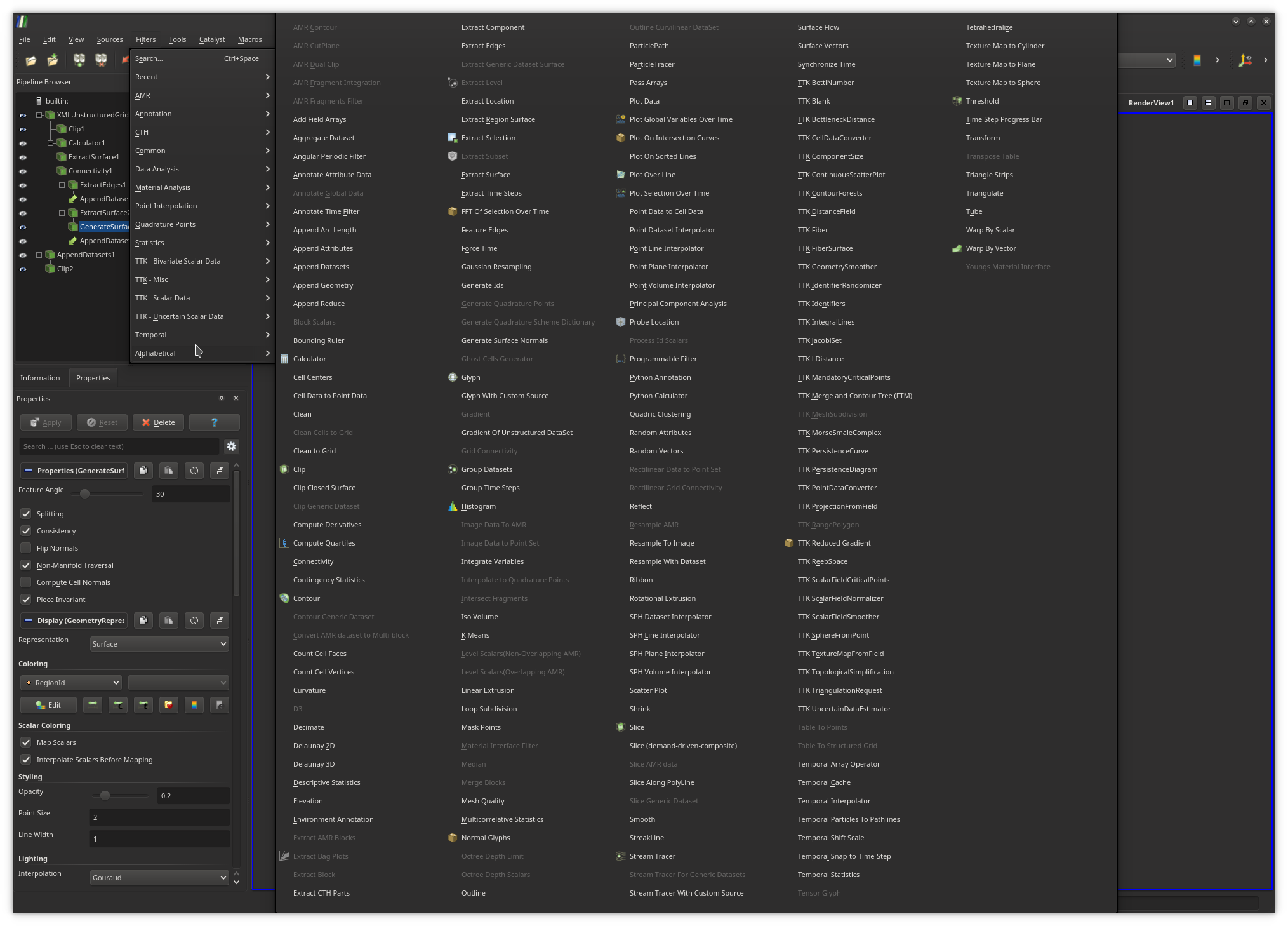
The output of each filter can be visualized independently (by toggling the eye icon, left column). The algorithmic parameters of each filter can be tuned in the "Properties" panel (bottom left panel) by selecting a filter in the pipeline (in the above example GenerateSurfaceNormals1). The display properties of the output of a filter in the main central view can also be modified from this panel.
To create a pipeline from scratch, users typically load their input data and apply successively the required filters, by browsing the filter menu (exhaustive list shown above), where the filters which are not compatible with the object currently selected in the pipeline are shaded.
Alternatively to the filter menu, users can toggle a fast search dialog by pressing the Ctrl+space keystroke (under Linux) and enter keywords as shown above to quickly call filters.

ParaView supports the rendering of multiple (possibly linked) views. To generate a new view, users simply need to click on the vertical or horizontal split buttons, located at the top right of the current render view. To link two views together (i.e. to synchronize them in terms of view point), users simply need to right-click in one of the two views, then select the Link Camera... entry and finally click in the other view they wish to link.

Once users are satisfied with their analysis and visualization pipeline, they can save it to disk for later re-use in the form of a Python script with the menu File, Save state... and choosing the Python state file type. In the Python script, each filter instance is modeled by an independent Python object, for which attributes can be changed and functions can be called.
Note that the output Python script can be run independently of ParaView (for instance in batch mode) and its content can be included in any Python code (the pvpython interpreter is then recommended). Thus, ParaView can be viewed as an interactive designer of advanced analysis Python programs. To learn more about the available ParaView filters, please see the following tutorials: HERE and THERE.

In the following, it is highly recommended to regularly save the current status of your analysis, by saving a .pvsm state file with the menu File, Save state... (ideally, on file per exercise).

3. Generating some toy data

Exercise 1

In the first part of this tutorial, we will experiment with some toy 2D data that we will synthesize ourselves. Open ParaView and simply call the Plane filter (also available in the Sources menu). Create a new plane with sufficient values for the parameters XResolution and YResolution (typically 100 each).

ParaView supports real-time interfacing with the Python scripting language. For instance, by calling the Programmable Source or the Programmable Filter, users can directly type in Python commands to either create or interact with data. We will make use of similar features to create some 2D data to attach to our plane. 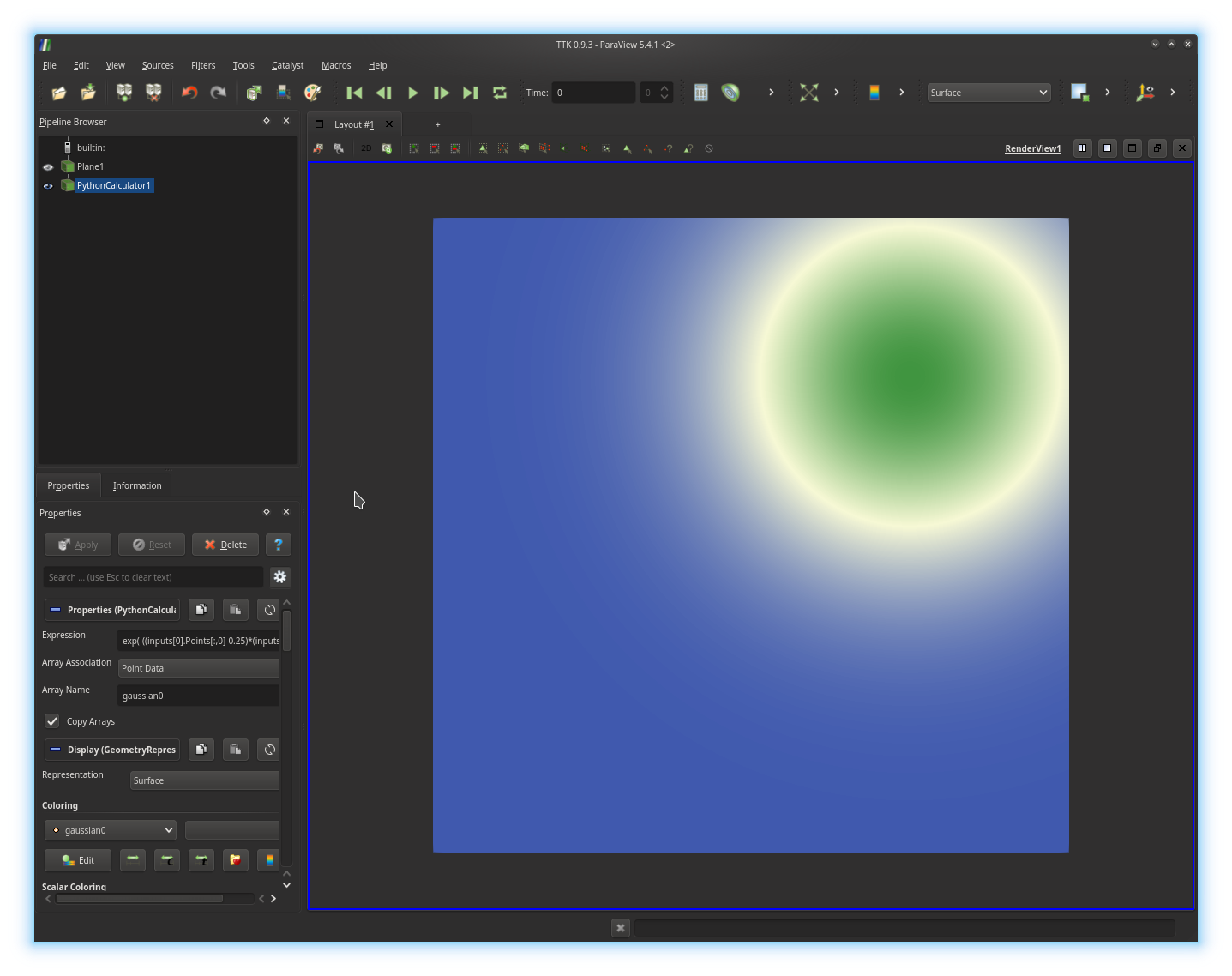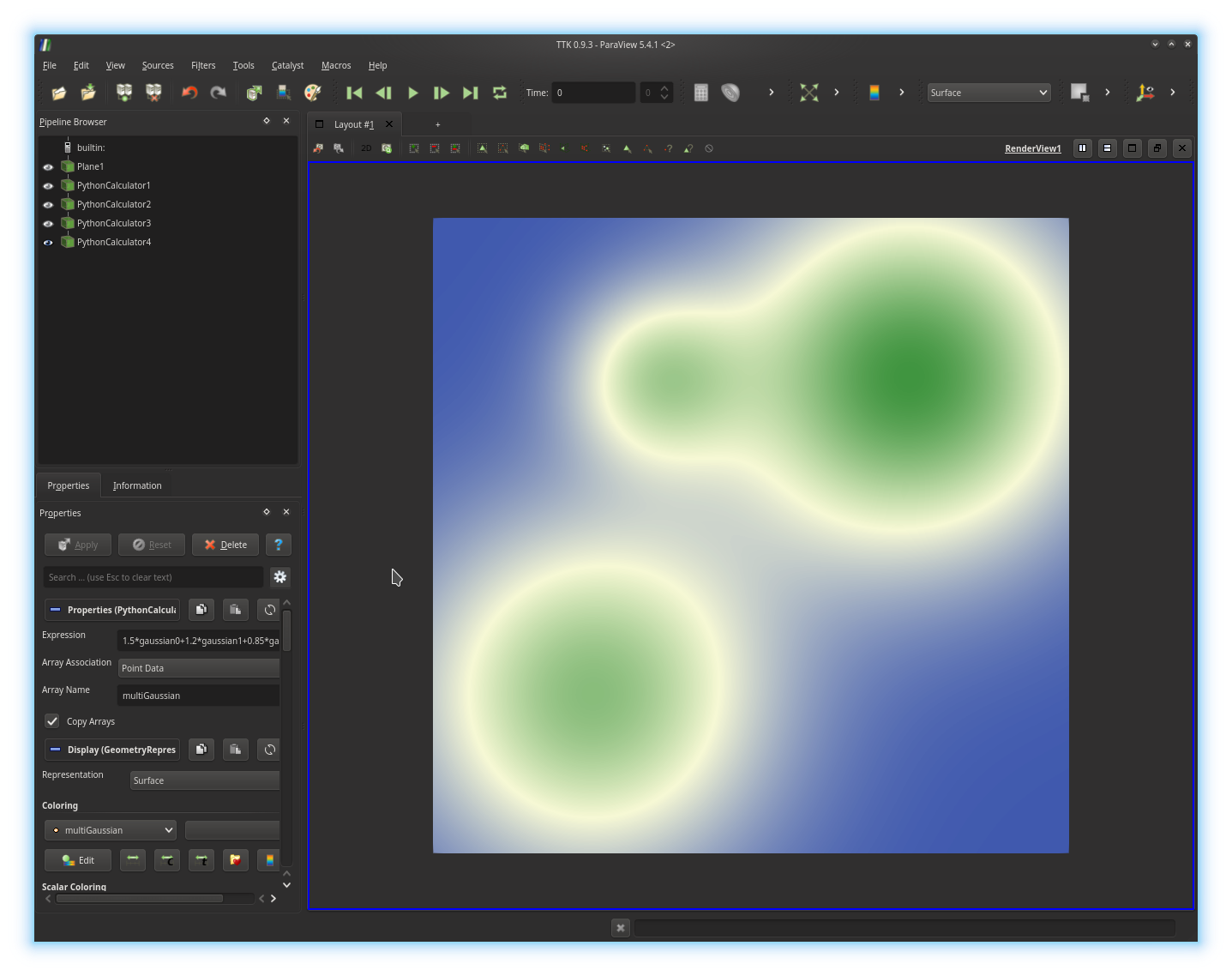Specifically, we will use the Python Calculator, which will enable us to provide, in Python, the analytic expression of a 2D function to be considered as the input to our topological data analysis pipeline.

In particular, we will create a Gaussian function, given by the expression:

$f(p) = e^{-{{||p - \mu||^2_2}\over{2\sigma^2}}}$

where $p$ is the current point where to evaluate the function, and where $\mu$ and $\sigma$ are the mean and standard deviation of the Gaussian.

In ParaView, each filter can have multiple inputs. In Python, the first input of our Python Calculator filter can be accessed by the variable inputs[0]. The actual points attached to this input can be accessed by its Points attribute: inputs[0].Points[]. Therefore, in your Python calculator, accessing the x and y components of your current point p can be done by considering the following expressions respectively: inputs[0].Points[:,0] (for x) and inputs[0].Points[:,1] (for y).

Use these expressions of the coordinates of the input points to evaluate in your Python Calculator the analytic expression of $f(p)$ given above, to generate a 2D Gaussian as shown in the example below (do not forget to name your function with a specific string for the Array Name parameter, typically gaussian0).
Now, re-iterate this process successively twice to create two other Gaussians, centered in other parts of the plane, with distinct standard deviations. Finally, use the Python Calculator to blend linearly the three Gaussians you generated into only one function, called multiGaussian, as illustrated below:

Exercise 2

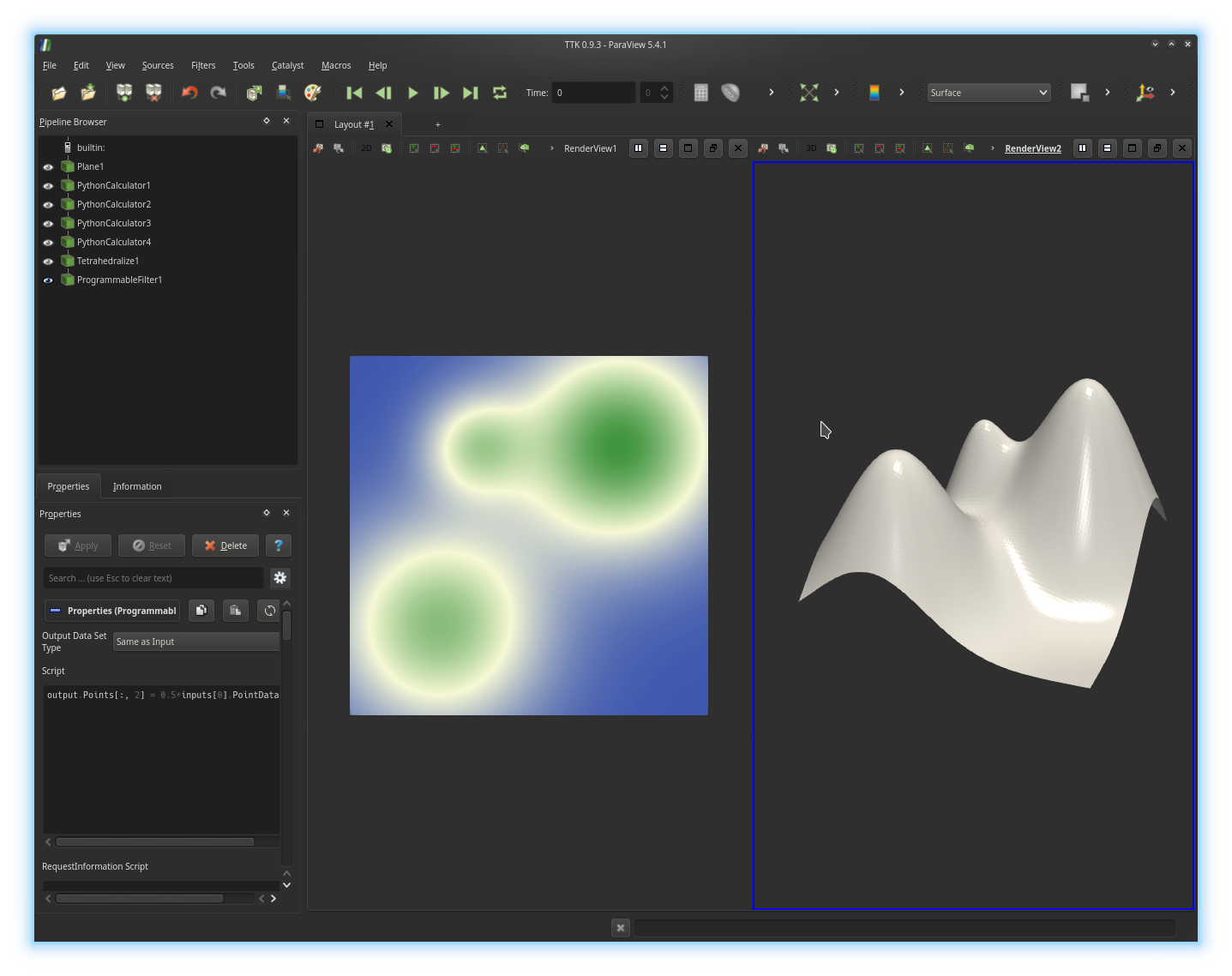
We will now inspect this toy data set as a 3D terrain. First, create a new render view, by clicking on the Split Horizontal button, located in the top right corner of the current render view (next to the string RenderView1). Next, in the newly created view, click on the Render View button.

To generate a 3D terrain, we will first triangulate the plane, which is currently represented as a 2D regular grid. For this, select the last Python Calculator object in your pipeline and call the Tetrahedralize filter on it. Next, we will modify the x, y and z coordinates of the vertices of this mesh to create a terrain.

To do this, we will use the Programmable Filter and enter some Python instructions to assign the previously define multi-gaussian function, named multiGaussian, as a z coordinate. Programmable Filters generate only one output, which is by default a copy of the input geometry. Thus, to access the output of your Programmable Filter, you need to use the Python expression output. Then, the z coordinate of the output can be accessed, similarly as to the previous exercise, by considering the Python expression output.Points[:, 2]. The scalar data that we generated in the previous exercise (multiGaussian) can be accessed by considering the field multiGaussian on the point data of the first input. This is achieved by considering the expression inputs[0].PointData["multiGaussian"].

Now enter the correct Python instruction in the Script text-box of your Programmable Filter to assign the multiGaussian value to the z coordinate of each point of the data and click on the Apply button. If you got it right, you should be visualizing something like this:
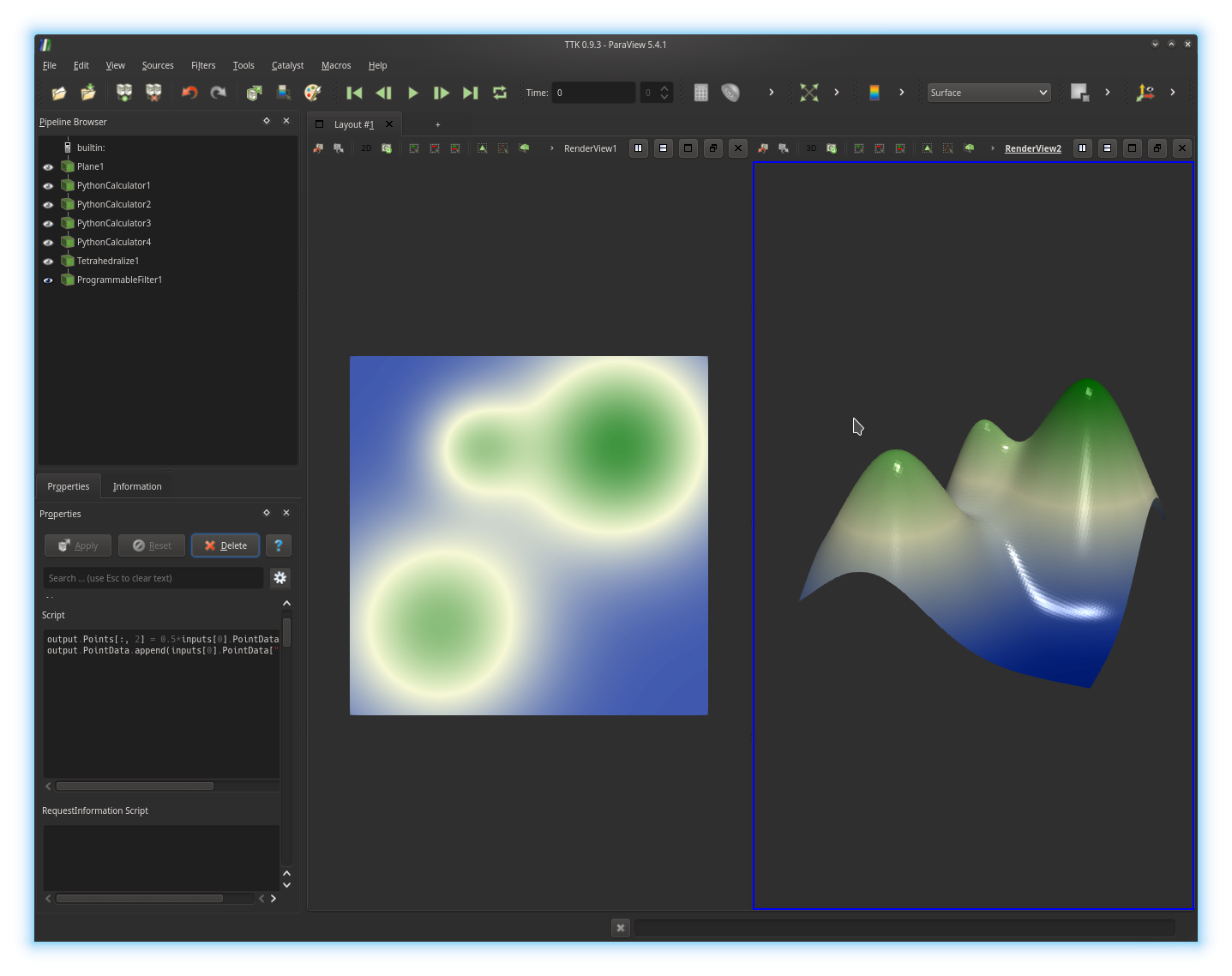
By default, the scalar fields attached to the input of our Programmable Filter have not been copied over to the output of the filter. We will now copy the field multiGaussian, in order to apply further processing on it. To add some data array to your output object, you need to use the function append() on your output.PointData object. This function takes as a first argument the actual data array (in our case inputs[0].PointData["multiGaussian"]) and as a second argument a string, used to name the created data array (in our case, let us name it multiGaussian too).

Add a second instruction in the Script text-box of your Programmable Filter to copy the field inputs[0].PointData["multiGaussian"] over to your output and click on the Apply button. If you got it right, you should be visualizing something like this:
Now, select the left render view (with the 2D version of your data), by clicking in it. Next, in the pipeline browser, trigger the display of the output of your Programmable Filter, by enabling the eye icon on its left. Adjust its display properties (Coloring, Specular, Ambient and Diffuse) to obtain a visualization comparable to the above screenshot.

4. Sub-level set homology

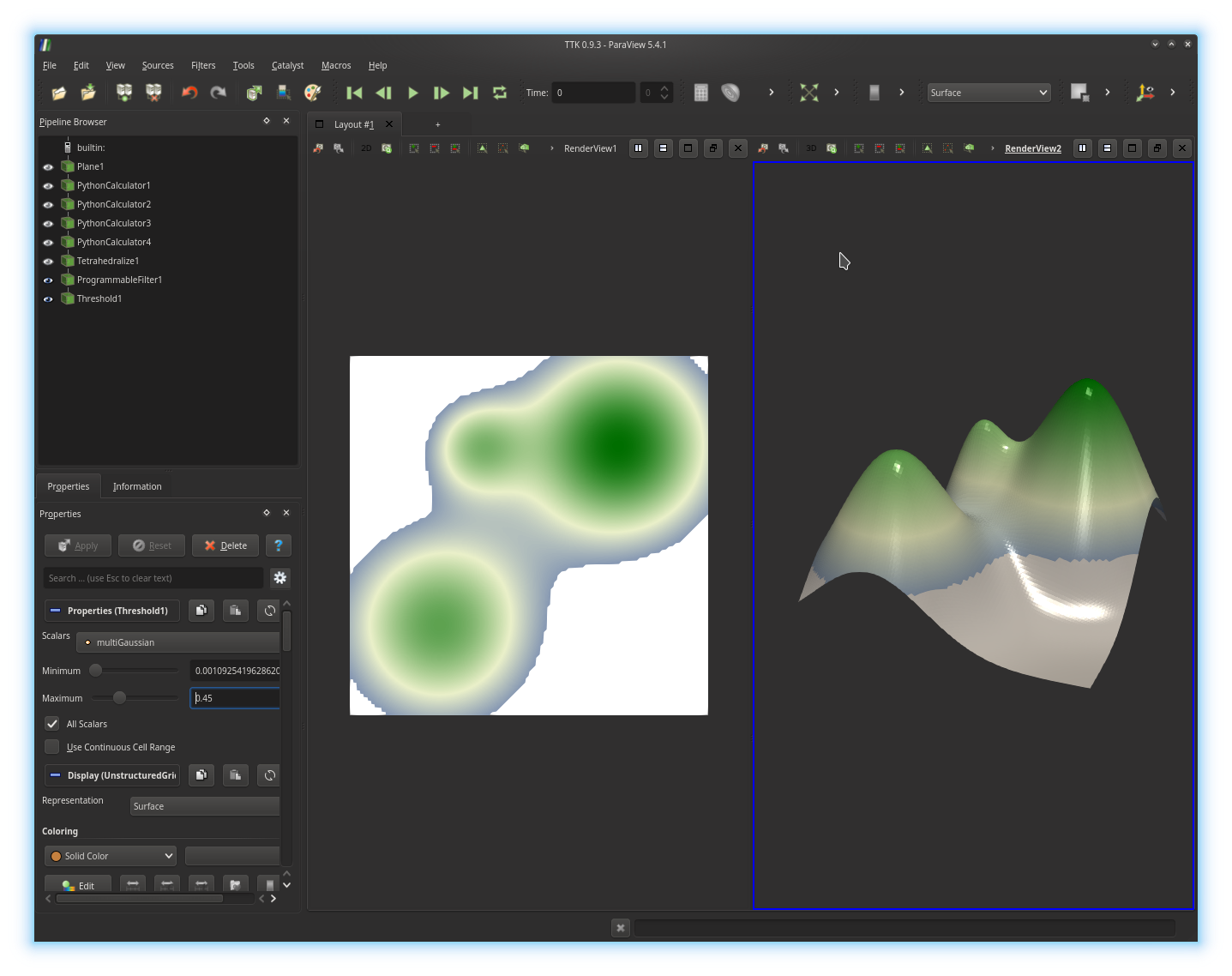
Exercise 3

We will now visualize and inspect the evolution of the topology (of the Betti numbers $\beta_0$ and $\beta_1$) of the sub-level sets $f^{-1}_{-\infty}(i)$ as $i$ continuously sweeps the data. For further readings on persistent homology, see the following reference text book (page 190 of the PDF file) or the following course notes .

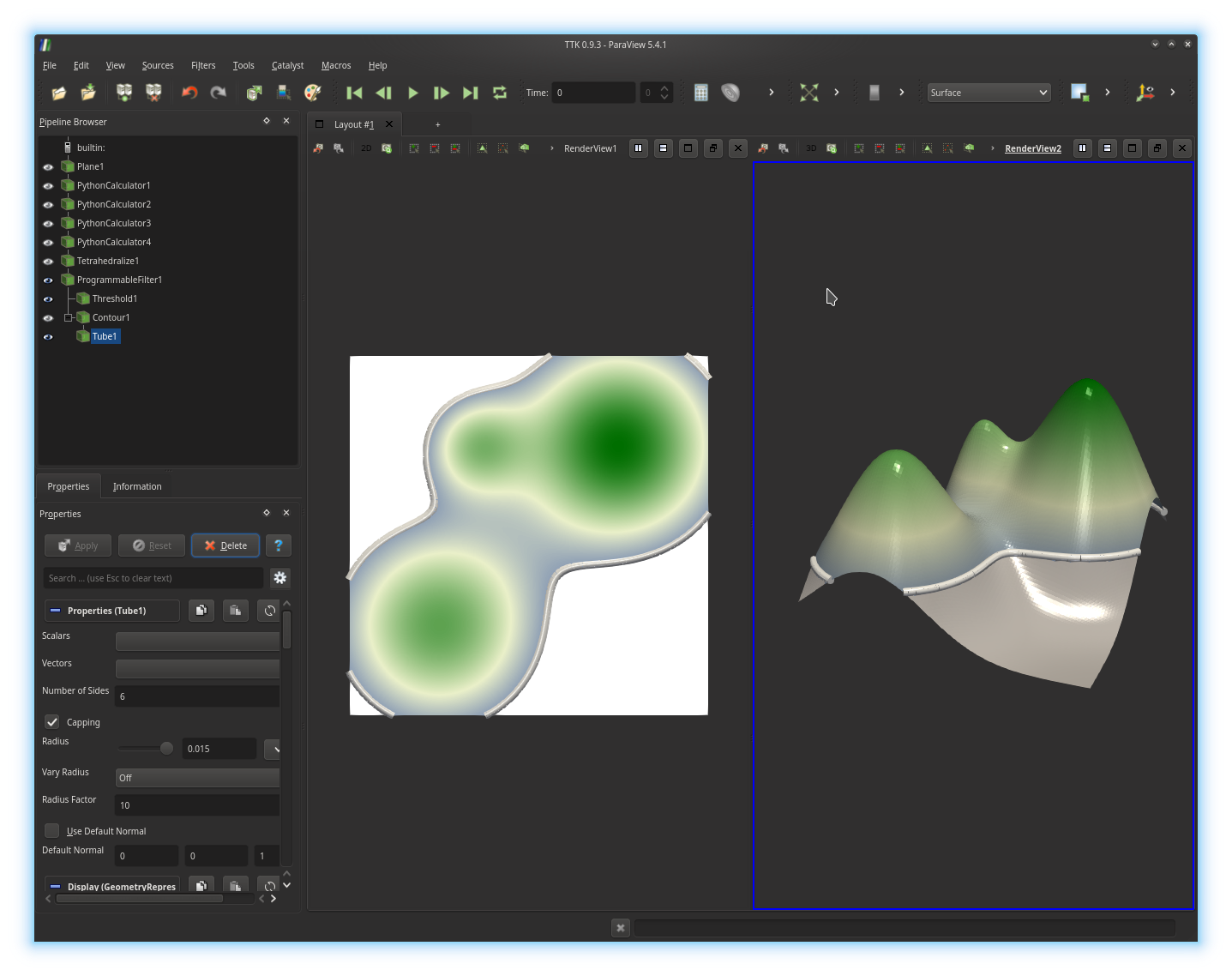
In the pipeline browser, select your Programmable Filter and call the Threshold filter, to only select the points below on certain isovalue of multiGaussian. Trigger the display of the Threshold in both views, to obtain the following visualization:
We will additionally compute and display the level set at the same isovalue: $f^{-1}(i)$. For this, in the pipeline browser, select your Programmable Filter and call the Contour filter and extract a level set at the same isovalue. Next call the Tube filter on the output of the Contour filter, to represent the computed level set with a collection of cylinder primitives, in both views, as illustrated below:

Exercise 4

We will now animate the sweeping of the data and visualize the corresponding animation.

In the View menu, check the Animation View check-box. The Animation View panel appears at the bottom of the screen. We will first setup the length of the animation by setting the EndTime parameter to 10 (seconds). Next, we will set the frame rate to an admissible value (25 fps) and therefore set the parameter No. Frames to 250.

We will now specify which parameters of our visualization should vary during the animation. In particular, we want the isovalue (of the sub- and level sets) to continuously increase with time. For this, at the bottom left of the Animation View, next to the + icon, select your Threshold filter in the left scrolling menu and then, within the right scrolling menu, select its parameter capturing the isovalue (Threshold Range (1)) and click on the + button. Next, also add the Contour filter to the animation by selecting it in the bottom left scrolling menu and by clicking on the + button (the default selected parameter Isosurfaces is precisely the parameter we want to animate).

Your animation is now ready to play!
Go ahead and click on the Play button at the top of the screen. If you got it right, you should be visualizing something like this:
For what isovalues $i$:
   ·  does $\beta_0(f^{-1}_{-\infty}(i))$ increase?
   ·  does $\beta_0(f^{-1}_{-\infty}(i))$ decrease?
   ·  does $\beta_1(f^{-1}_{-\infty}(i))$ increase?
   ·  does $\beta_1(f^{-1}_{-\infty}(i))$ decrease?

Exercise 5

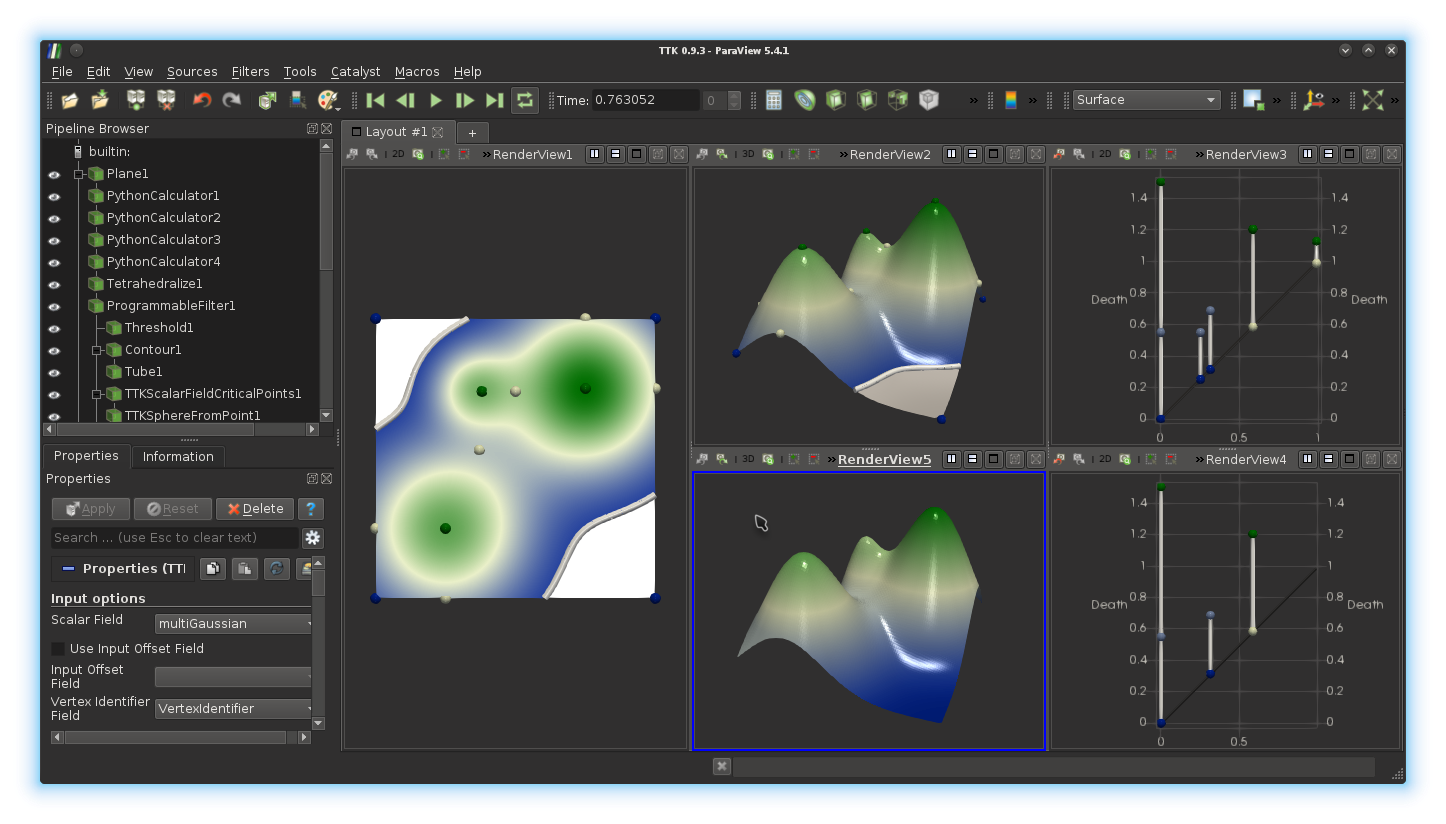
We will now identify the exact locations in the data where the Betti numbers of $f^{-1}_{-\infty}(i)$ change.

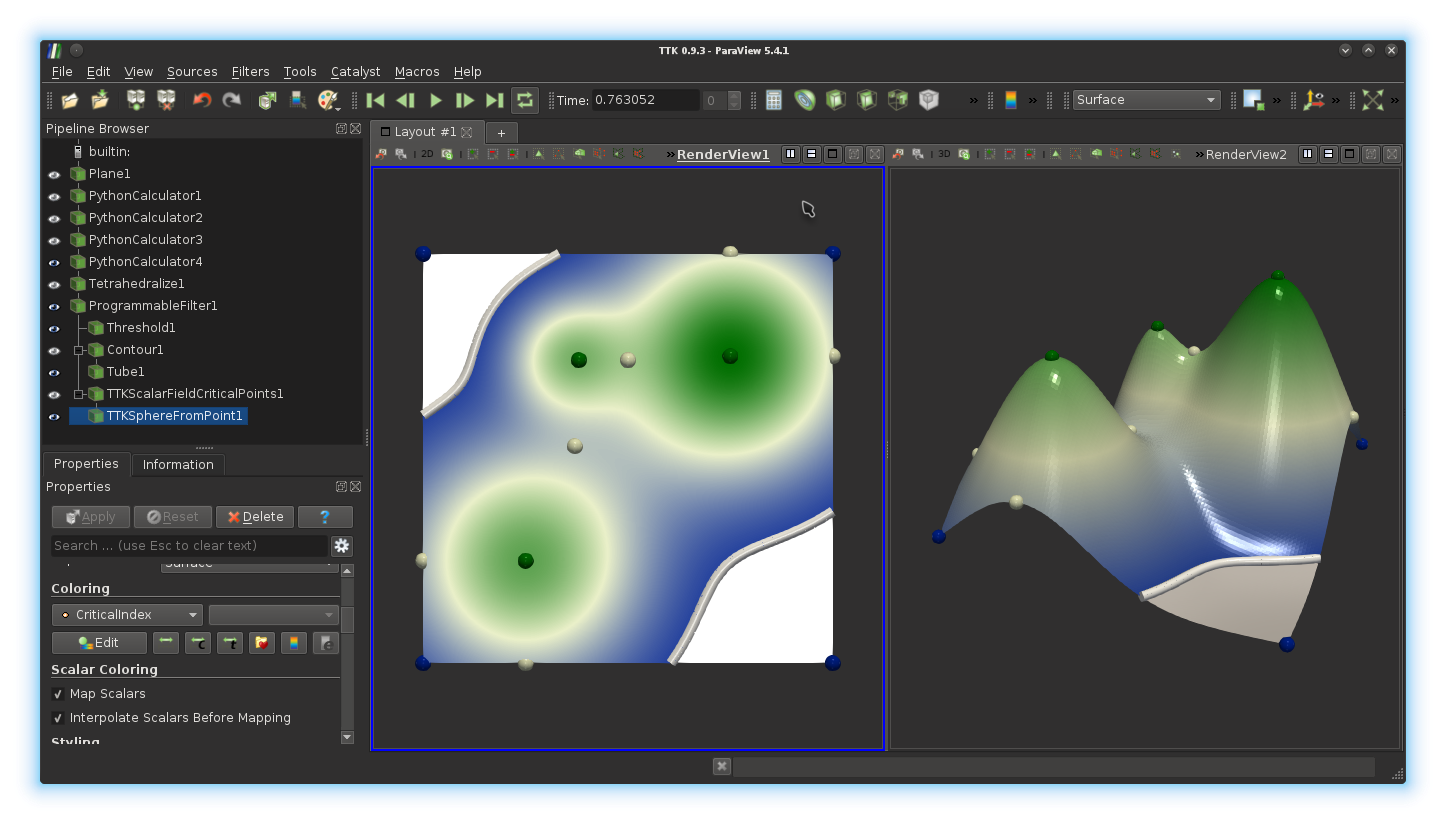
Select the view with the 3D terrain by clicking in it. In the pipeline browser, select the output of your Programmable Filter and call the filter TTK ScalarFieldCriticalPoints on it.
The output of this filter is a point cloud that may be difficult to visualize by default. We will enhance this visualization by displaying a visual glyph for each point, in particular, a sphere. Call the filter TTK SphereFromPoint filter on the output of the TTK ScalarFieldCriticalPoints filter and adjust the Radius parameter. Next, change the coloring of these spheres, in order to use the array CriticalIndex. Finally, select the 2D view on the left by clicking in it and trigger the display of these spheres, with the same display properties. If you got it right, you should be visualizing something like this:
How does the field CriticalIndex (color-coded on the spheres) relate to:
   ·  the increase of $\beta_0(f^{-1}_{-\infty}(i))$?
   ·  the decrease of $\beta_0(f^{-1}_{-\infty}(i))$?
   ·  the increase of $\beta_1(f^{-1}_{-\infty}(i))$?
   ·  the decrease of $\beta_1(f^{-1}_{-\infty}(i))$?

5. Persistent homology

Exercise 6

We will now inspect this data from the view point of persistent homology.

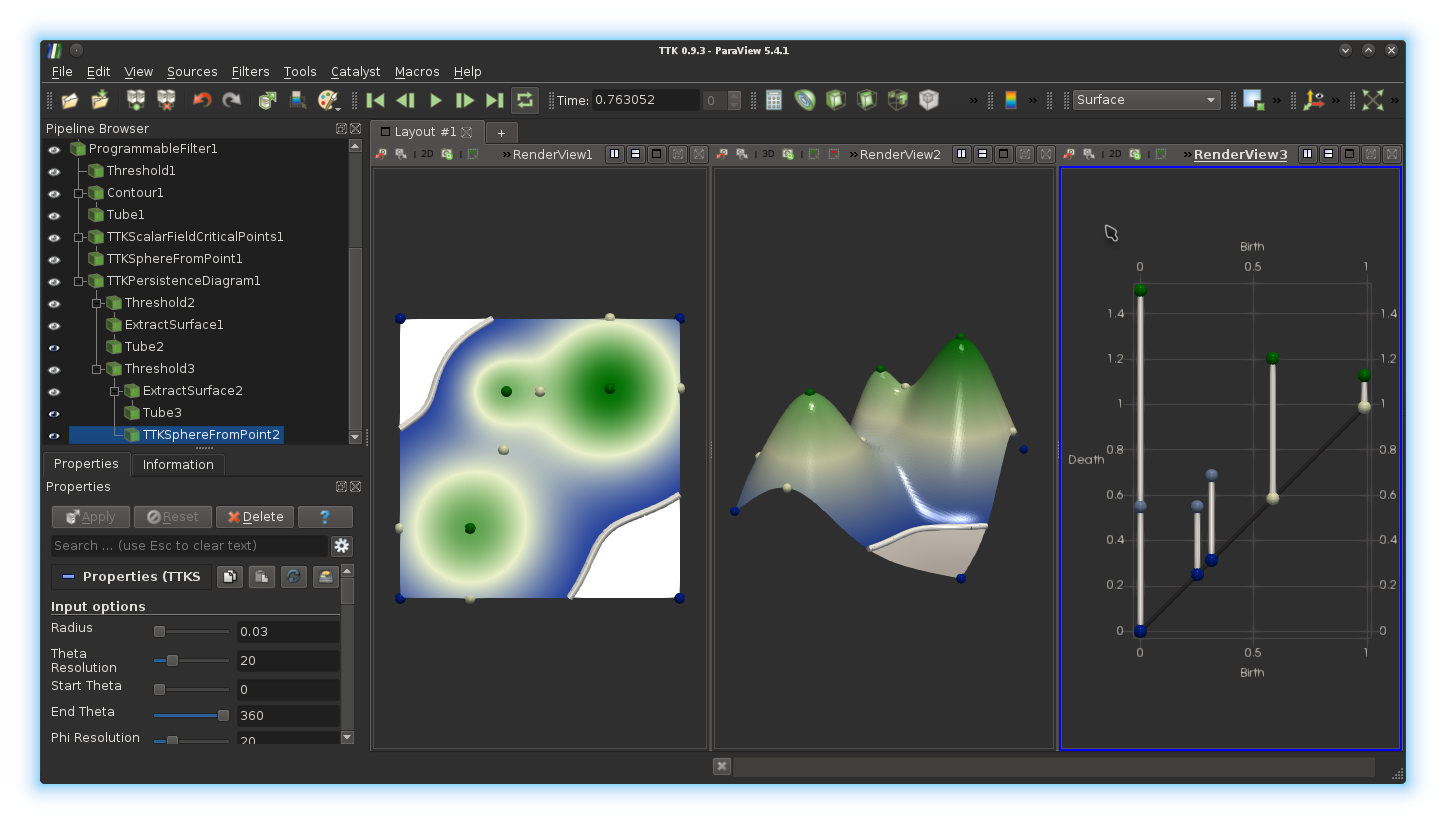
Create a third view on the right by clicking on the Split Horizontal button, located at the top right corner of the right render view (next to the string RenderView2) and then click on the Render View button.

In the pipeline browser, select the output of your Programmable Filter and call the filter TTK PersistenceDiagram on it. A persistence diagram should display in the newly created view.

The visualization of the persistence diagram can be improved in several ways. First, in the display properties of the TTK PersistenceDiagram filter, enable the display of the axes by checking the Axes Grid check-box (you can tune its parameters, such as the name of the axes by clicking on the Edit button next to it).

Next, we will improve the visualization of the diagram itself. By default, the diagram embeds a virtual edge representing the diagonal. This virtual edge can be filtered out to be removed from the visualization or to be visualized with a distinct color. This virtual edge can be isolated from the others as it is the only edge with a negative value for the field PairIdentifier. Use the Threshold filter on the output of the TTK PersistenceDiagram filter to isolate this edge. Next, convert your selected edge to a polygonal surface representation by calling the Extract Surface filter on it. Finally, represent this edge with a cylinder primitive by calling the Tube filter (adjust the Radius and coloring properties).

Next, we will also display the actual persistent pairs with cylinders. For this, in the pipeline browser, select the output of the TTK PersistenceDiagram filter and apply the Threshold filter on it to only display these pairs with non-negative values for the field PairIdentifier. Next, convert this selection into a polygonal surface representation by calling the Extract Surface filter and represent these edges with cylinder primitives by calling the Tube filter (adjust the Radius and coloring properties).

Finally, we will represent each extremity of a persistence pair by a visual glyph, in particular, a sphere. For this, in the pipeline browser, select the output of the Threshold filter which selected the pairs with non-negative identifiers in the diagram and apply the TTK SphereFromPoint filter on it. Adjust the radius and set the coloring to use the field NodeType. If you got it right, you should be visualizing something like this:
Given the persistence diagram on the right, identify in the original data (on the left) the least persistent critical point pairs responsible for changes in $\beta_0(f^{-1}_{-\infty}(i))$ and $\beta_1(f^{-1}_{-\infty}(i))$ respectively.

Exercise 7

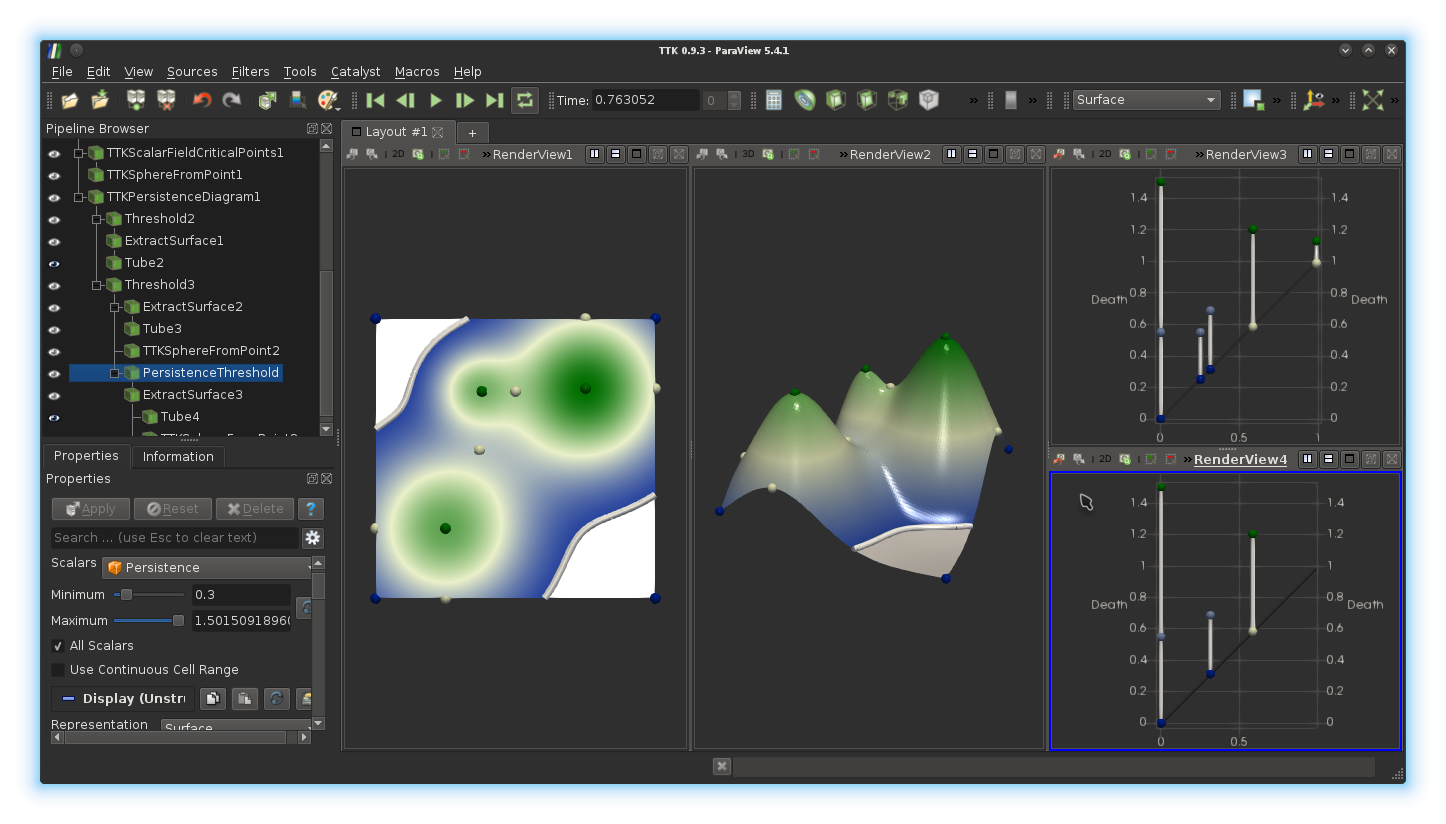
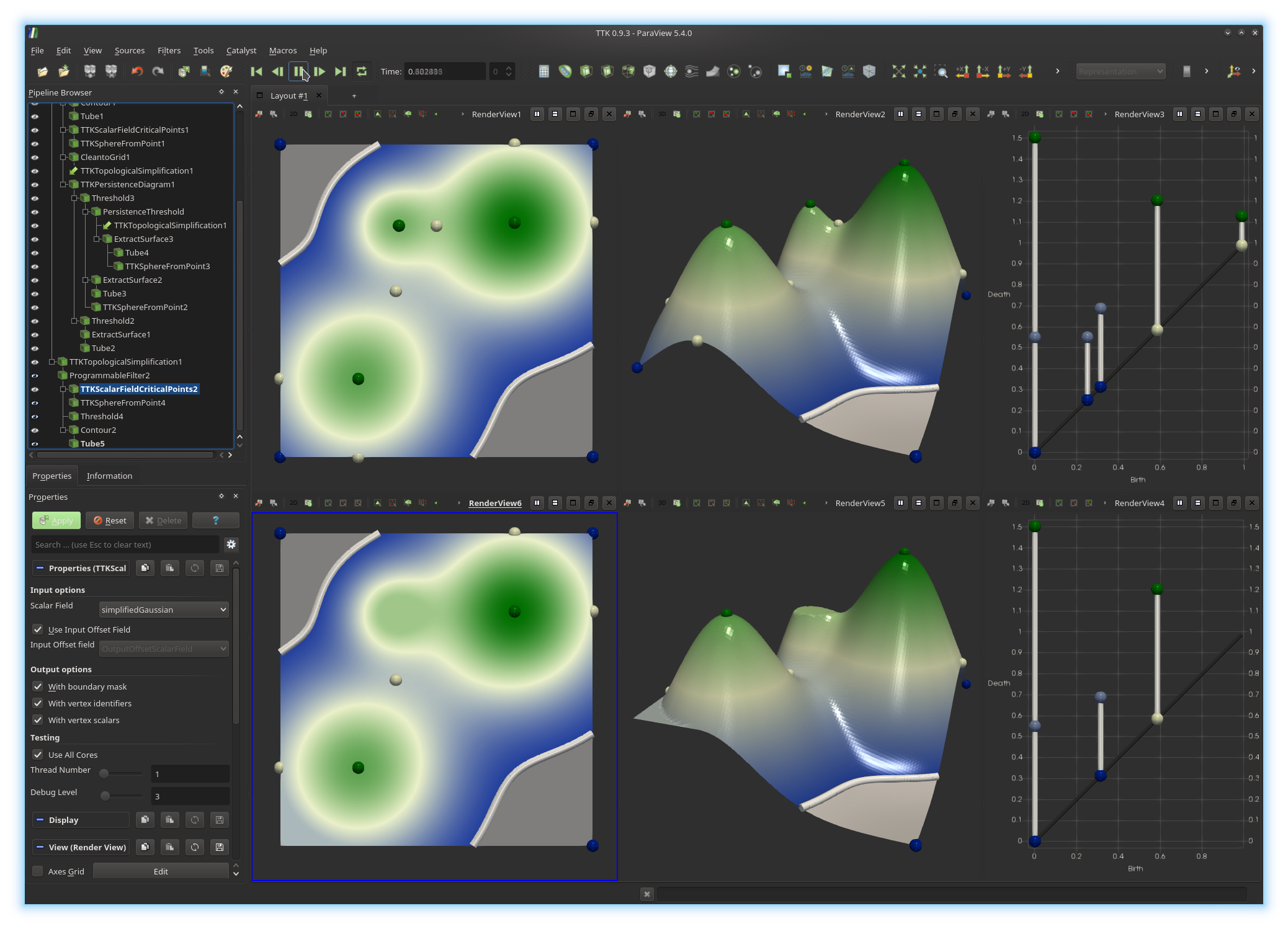
We will now illustrate stability results on the persistence diagram and experiment with persistence-sensitive function simplification.

Split the render view containing the persistent diagram using the Split Vertical bottom (top right corner, second button after the string RenderView3 and click on the Render View button. In this view, display the diagonal of the persistence diagram as well as the persistence pairs more persistent than the two pairs identified in the previous question (use the Threshold filter on the Persistence array to isolate those, as the pairs above a given persistence threshold and below an arbitrarily high threshold, for instance 9999). Enhance the visualization, as suggested in the previous question. If you got it right, you should be visualizing something like this:
We will now reconstruct a function $g : \mathcal{M} \rightarrow \mathbb{R}$ that admits this simplified persistence diagram $\mathcal{D}(g) \subset \mathcal{D}(f)$.

Before reconstructing the function $g$, we will first make a copy of the original function, that we will simplify. For this, in the pipeline browser, click on your Programmable Filter and add a Python instruction in the Script text-box to add a new field named simplifiedGaussian which is a copy of the field multiGaussian (see exercise 2). Next, apply the filter Clean to Grid on the output of your Programmable Filter, which will effectively perform the data copy.

Next, select the render view with the 3D terrain by clicking in it and split it vertically, using the Split Vertical bottom (top right corner, second button after the string RenderView2 and click on the Render View button. Now, in the pipeline browser, select the output of the Clean to Grid filter and call the filter TTK TopologicalSimplification on it. A dialog window opens to specify the two inputs of this filter. The first input, named Domain (see the left ratio buttons), should already be set properly to your Clean to Grid filter. The second input, named Constraints (see the left ratio buttons), refers to the persistent pairs which we want to keep in the reconstructed function $g$. These correspond to the apparent edges in the simplified persistence diagram $\mathcal{D}(g) \subset \mathcal{D}(f)$. Therefore, for this input, you should select in your pipeline the Threshold filter you used to select the most persistent pairs of the first diagram $\mathcal{D}(f)$. Once this is done, click on Ok. Now, before clicking on the green Apply button, in the properties panel, check the Numerical Perturbation check-box, make sure that you are applying the simplification to the scalar field simplifiedGaussian and click on Apply . Link this terrain view with the one above by right clicking in the bottom view, selecting the entry Link Camera... and then clicking on the top view. If you got it right, you should be visualizing something like this:
Similarly to the exercise 2, we will now modify the geometry of the terrain, such that the z coordinate of each point becomes equal to the simplified function $g$, named simplifiedGaussian. For this, select the filter TTK TopologicalSimplification in the pipeline browser and call a Programmable Filter on it and apply the same processing as in the exercise 2 (but on our new field simplifiedGaussian). Do not forget to copy the fields simplifiedGaussian and multiGaussian. Also, the filter TTK TopologicalSimplification generates an offset field (or tiebreak field) named OutputOffsetScalarField. Make sure to also copy this field, as it is necessary to further process the simplified data properly.
Update: as of version 0.9.6, this field is name ttkOffsetScalarField by default.

Now split the left view vertically, using the Split Vertical bottom (top right corner, second button after the string RenderView1 and click on the Render View button. Click now on the 3D icon (top left corner of the view) to switch it to 2D and trigger the display of the output of the second Programmable Filter in it. Adjust its display properties (Coloring, Specular, Ambient and Diffuse) to obtain a visualization that is consistent with the above view. Link this 2D bottom view with the above one (right click, Link Camera...).

Next, we will extract the critical points of $g$ and visualize them in both bottom views (2D plane and 3D terrain). In the pipeline browser, select the output of the second Programmable Filter and call the filter TTK ScalarFieldCriticalPoints. Before clicking on the Apply button, check the check-box Use Input Offset Field and make sure you are applying this filter to the scalar field simplifiedGaussian. Finally, enhance this visualization by displaying a sphere for each critical point, colored by its critical index, with TTK SphereFromPoint, and display these spheres in both bottom views (2D plane and 3D terrain).
Update: as of version 0.9.6, there is no need to check the box UseInputOffsetField. Input offsets are now automatically retrieved from the data, if present. To force the usage of a specific field as vertex offset (advanced usage), check the box ForceInputOffsetField.

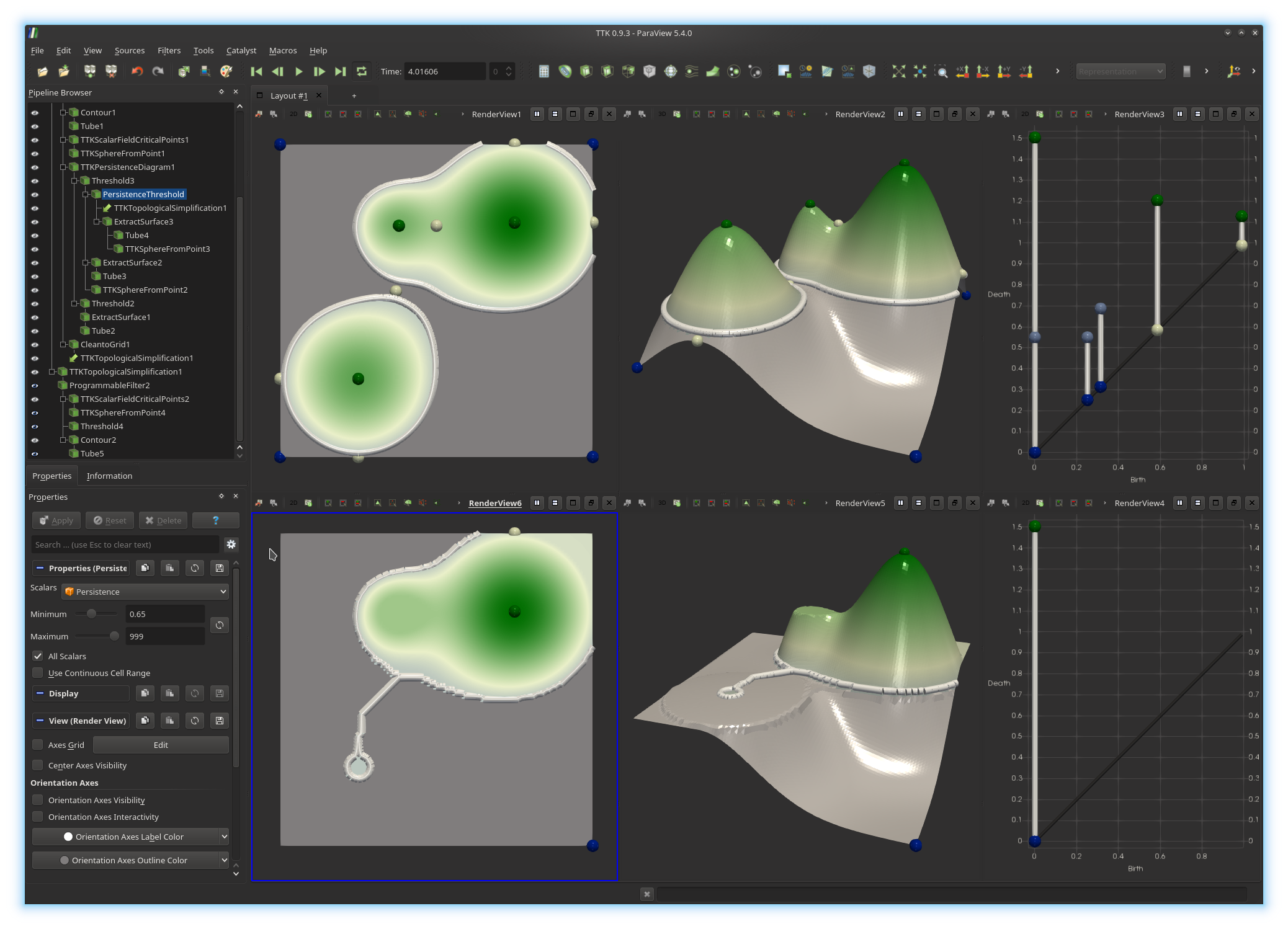
Finally, we will extract and animate the sub-level sets $g^{-1}_{-\infty}(i)$ and level sets $g^{-1}(i)$ of $g$, to visually compare them with these of $f$. In the pipeline browser, select the output of the second Programmable Filter and, similarly to exercise 3, call the Threshold filter on it to display $g^{-1}_{-\infty}(i)$ in both bottom views (2D plane and 3D terrain) and adjust display properties in 2D. Next, in the pipeline browser, select the output of the second Programmable Filter again and call the Contour filter on it to extract $g^{-1}(i)$, followed by the Tube filter (to display it with cylinder primitives) and trigger its display in both bottom views (2D plane and 3D terrain). We will now complete the animation by animating the isovalue $i$ for both $g^{-1}_{-\infty}(i)$ and $g^{-1}(i)$. In the View menu, check the Animation View check-box and similarly to exercise 4, add $g^{-1}_{-\infty}(i)$ and $g^{-1}(i)$ to the animation.

At this point, your animation is ready to play!
Go ahead and click on the Play button at the top of the screen. If you got it right so far, you should be visualizing something like this:
Now, in the pipeline browser, select the Threshold filter with which you controlled the persistence threshold (beginning of exercise 7) and increase that threshold until $g$ admits only one maximum. Play the animation and inspect the shape of $g^{-1}_{-\infty}(i)$ in the vicinity of the canceled maxima. You should be visualizing something like this:
How can you explain this visual artifact?

In the TTK TopologicalSimplification filter, un-check the check-box Numerical Perturbation and click on Apply. How can you explain the disappearance of the artifact?

Exercise 8

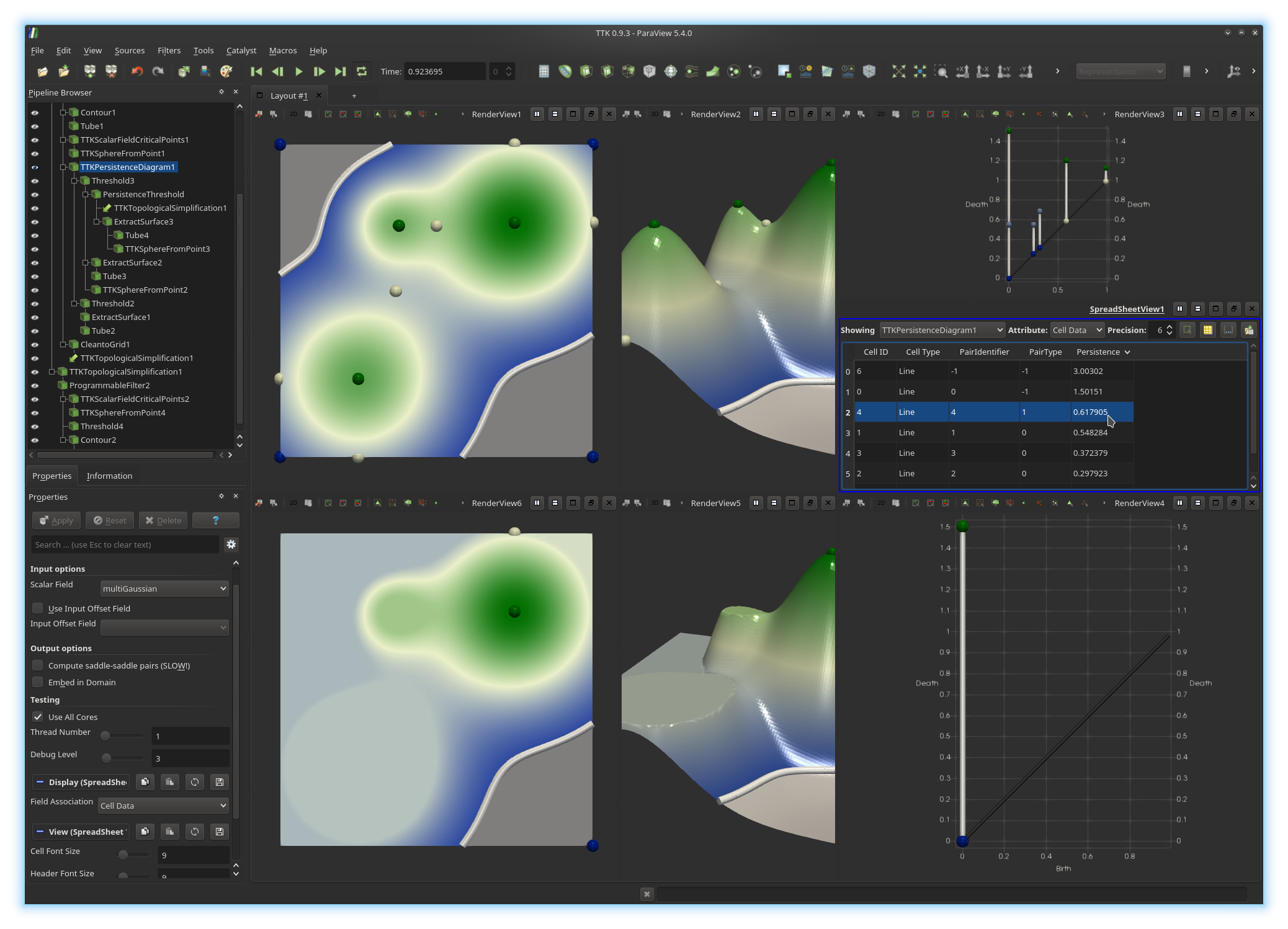
We will now inspect the stability of the persistence diagram.

Split vertically the top right view (containing the original persistence diagram $\mathcal{D}(f)$) with the Split Vertical button and click on SpreadSheet View. In the scrolling menu named Showing, select from your pipeline the TTK PersistenceDiagram and select in the Attribute scrolling menu the entry Cell Data. This will display in a spreadsheet the information associated with each pair of the persistence diagram, including its persistence (last column), as shown below.
Sort the spreadsheet by persistence by clicking on the header of the corresponding column.
Now, write down the persistence of the most persistence pair which is absent from the bottom diagram below ($\mathcal{D}(g)$).

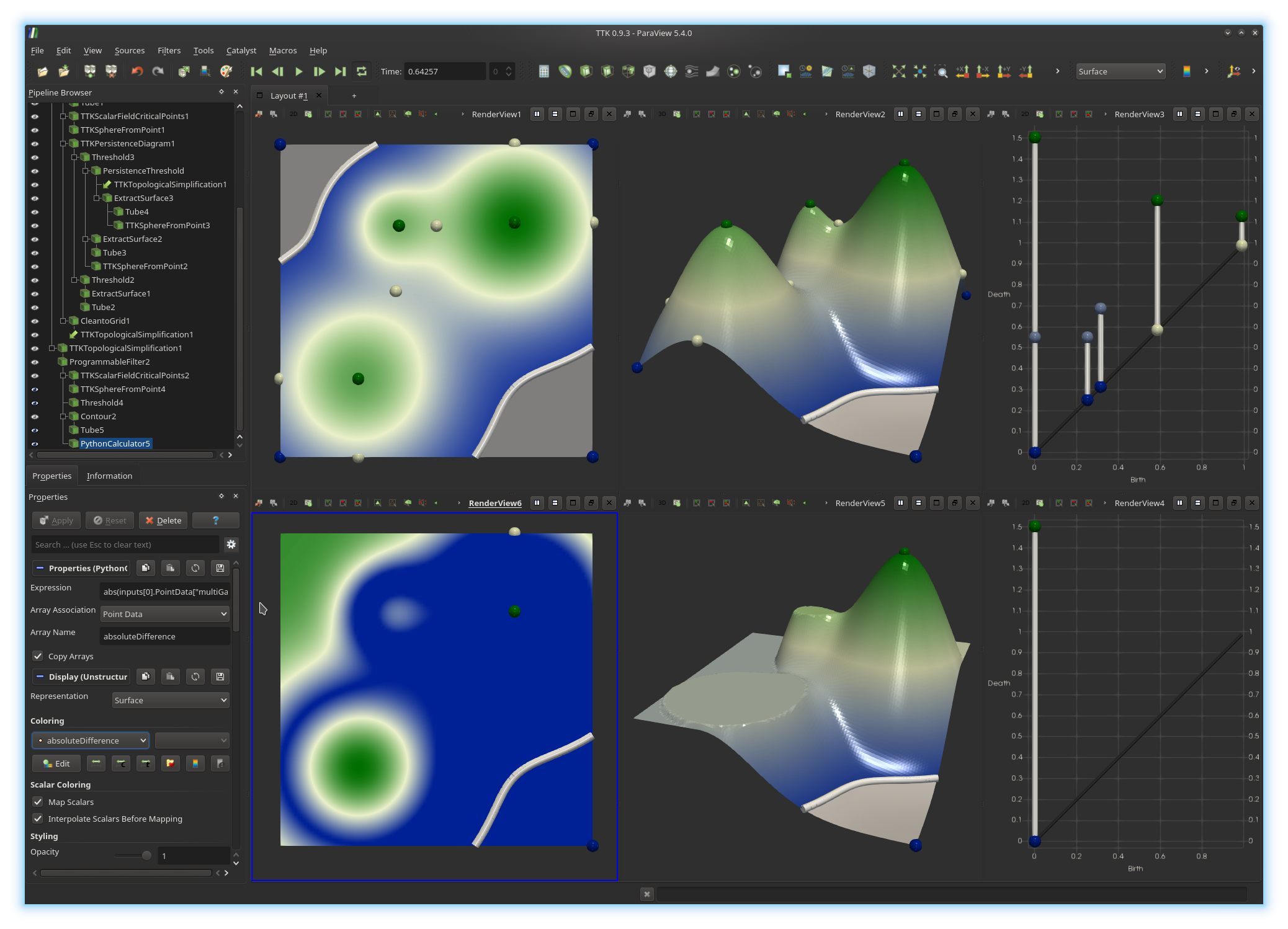
We will now evaluate $||f-g||_\infty$.
First, click in the bottom left view to activate it. Next, in the pipeline browser, select the output of the second Programmable Filter and call a Python Calculator on it. Now, enter the Python expression to evaluate $|f(p)-g(p)|$ for each point $p$ and call the output function absoluteDifference. If you got it right, you should be visualizing something like this:
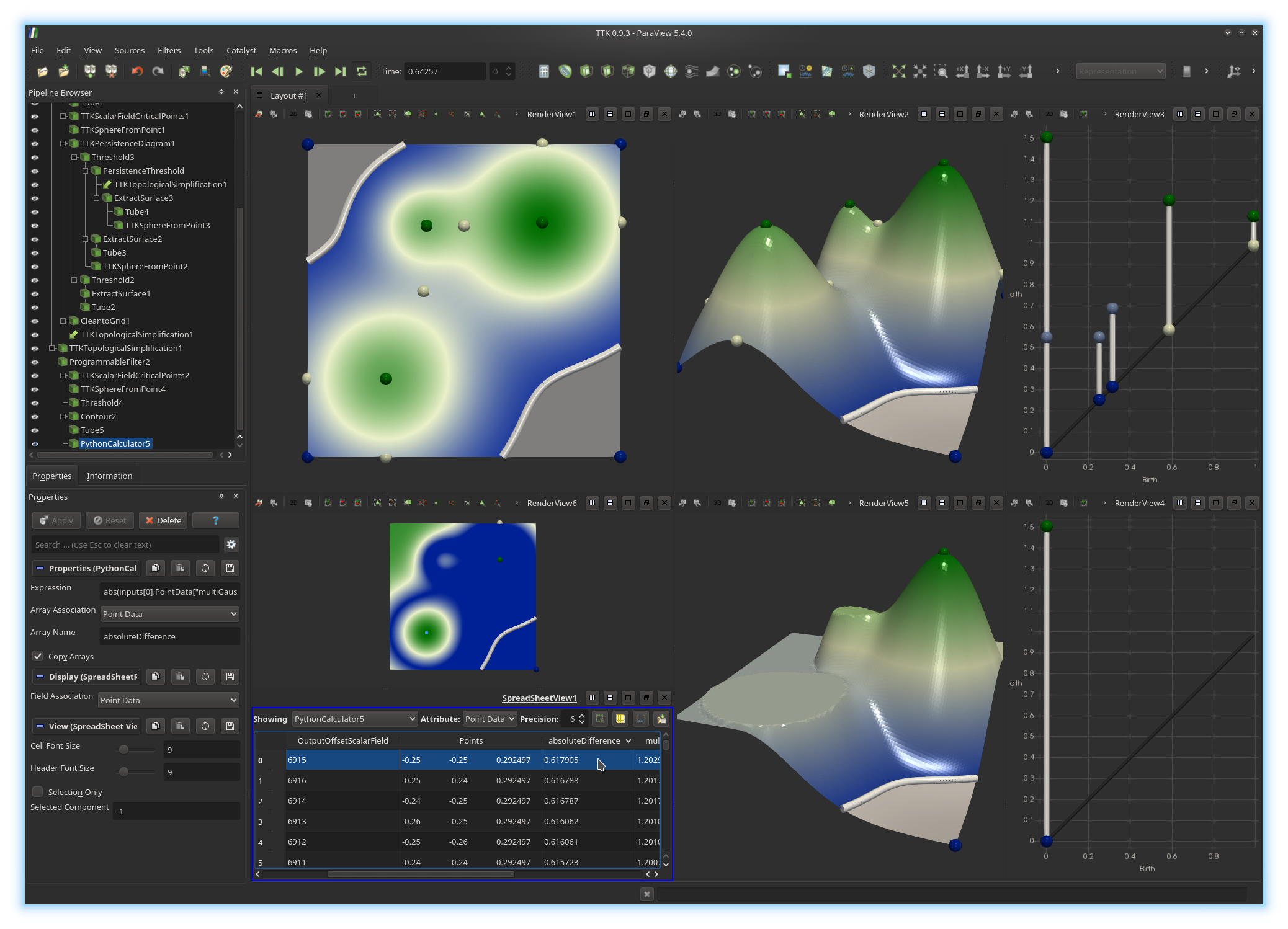
Now split the bottom left view vertically with the Split Vertical button and click on SpreadSheet View. In the scrolling menu named Showing, select from your pipeline the last Python Calculator. This will display in a spreadsheet the information associated with each vertex of the domain, including its absoluteDifference value, as shown below.
Sort the spreadsheet by absoluteDifference by clicking on the header of the corresponding column. Click on the spreadsheet entry that maximizes absoluteDifference. You should see the corresponding point highlighted in the above view.

What does this point correspond to?
How does its absolute difference value relate to the original persistence diagram?

6. Topological data segmentation

In our example, somehow, persistent homology helped us answer the following question:

What is the second highest mountain of my terrain?

We saw that the answer is not necessarily the second highest summit (second highest local maximum) but the second most persistent summit.

We will now combine persistent homology and split trees, in order to extract precisely the geometry of the second highest mountain of our terrain.

Exercise 9

Click in the top center view to activate it. Next, in the pipeline browser, select the output of the first Programmable Filter and call the filter TTK Merge and Contour Tree (FTM) on it (select Split Tree as Tree Type). This filter generates multiple outputs. Select the output Segmentation and change its Opacity to 0.3. Now, you should see an embedding of the split tree of your data. In the following, we will slightly enhance this embedding.

Modify the parameter Arc Sampling of your TTK Merge and Contour Tree (FTM) filter to a reasonable value (typically 10). Next, select its output Skeleton Arcs and call the filter TTK GeometrySmoother and check the box Use Input Mask Field. At this point, you may want to edit the number of smoothing iterations (typically to 30), to obtain a smoother embedding of the split tree. Next, we will display the arcs of the tree with cylinder primitives. For this, call the Extract Surface filter (to convert the arcs to a polygonal representation) and then the Tube filter. If you got it right, you should be visualizing something like this:
Now, go ahead and do the same thing for the simplified function in the bottom view. When calling the filter TTK Merge and Contour Tree (FTM), remember to use the simplifiedGaussian field and to check the box Use Input Offset Scalar Field. At this point, you may want to reduce the persistence threshold (beginning of exercise 7), to obtain a visualization like this one:
Update: as of version 0.9.6, there is no need to check the box UseInputOffsetField. Input offsets are now automatically retrieved from the data, if present. To force the usage of a specific field as vertex offset (advanced usage), check the box ForceInputOffsetField.

Exercise 10

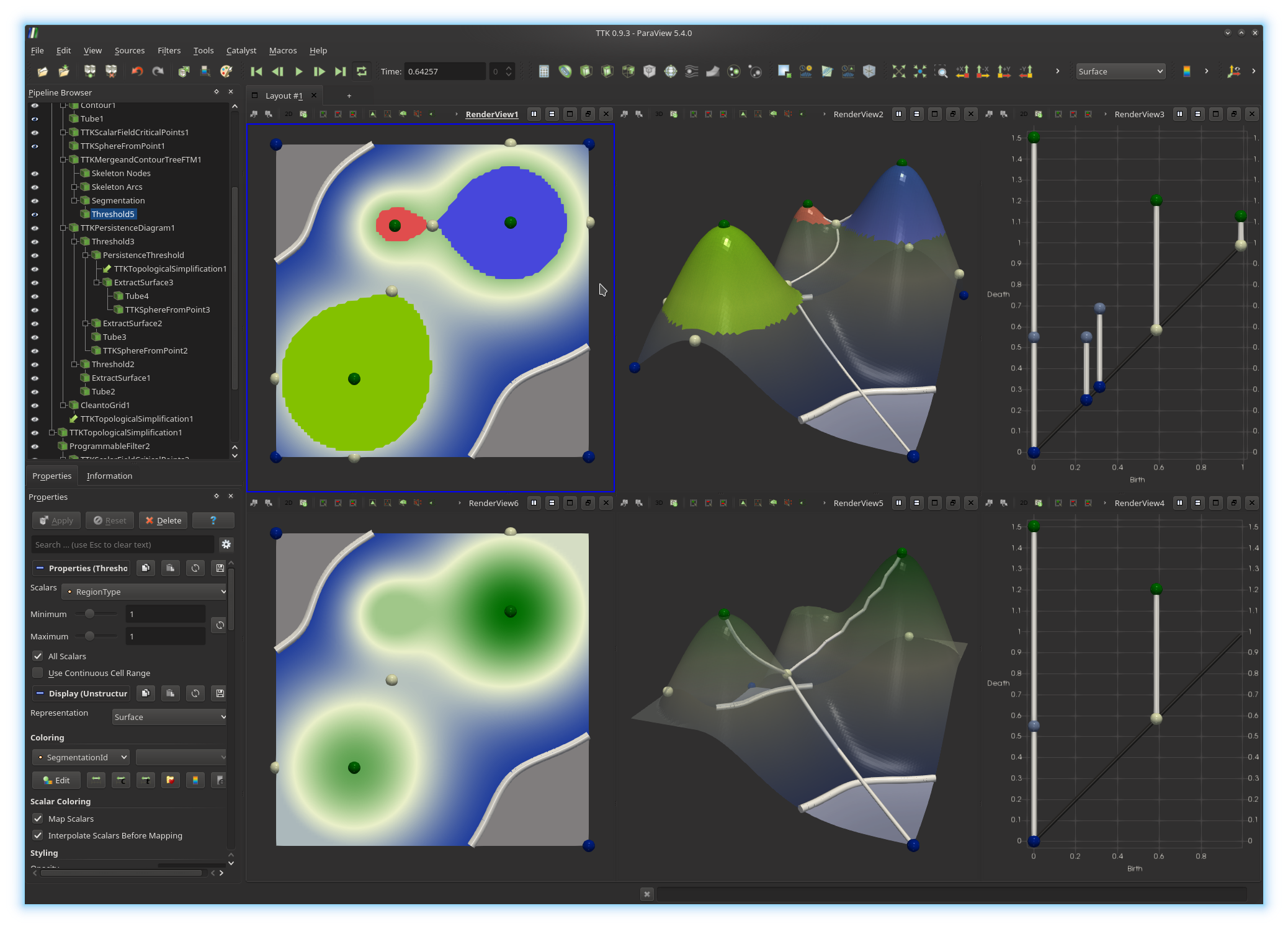
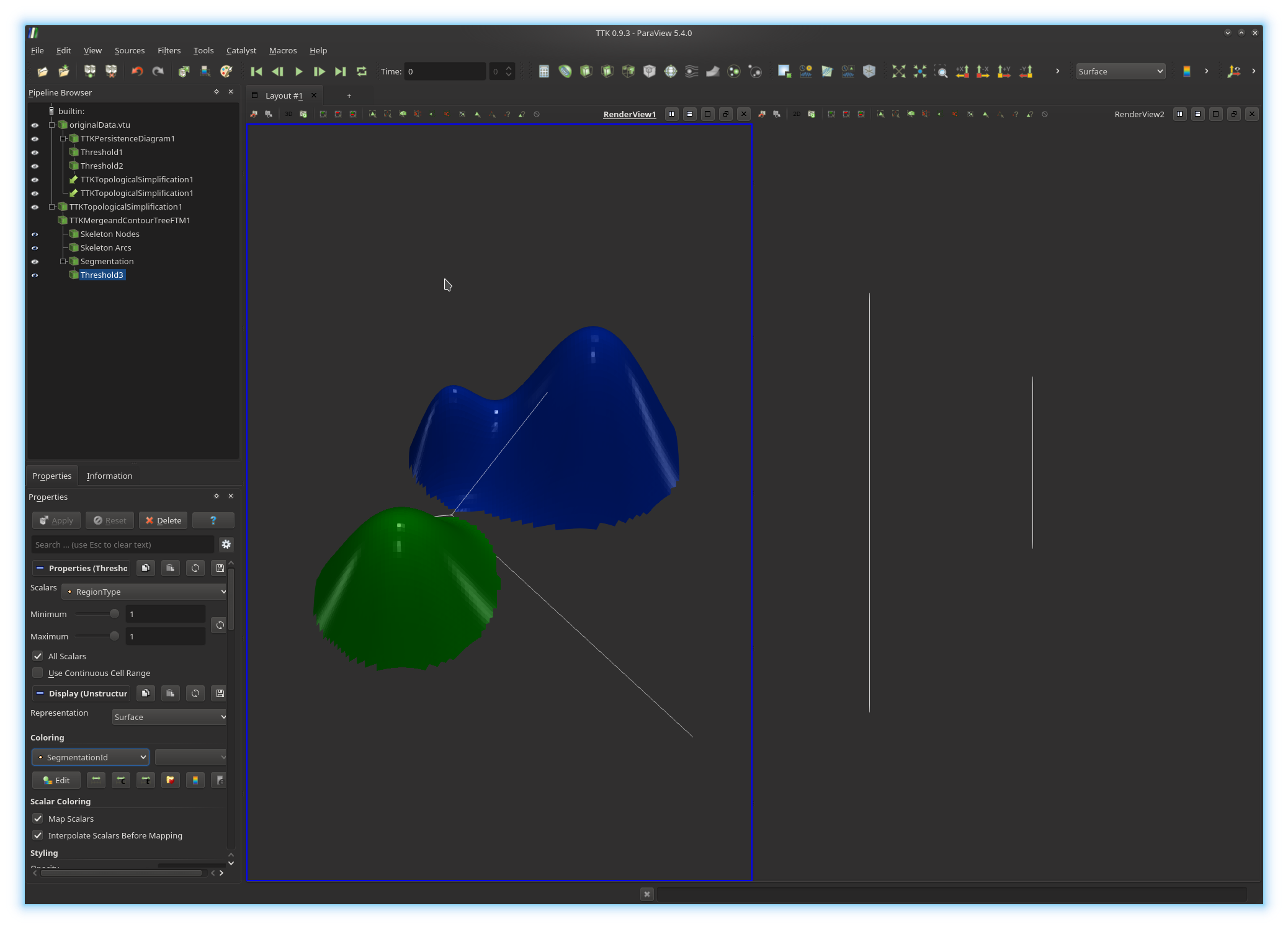
Thanks to the split tree, the geometry of each mountain can be extracted by collecting the set of vertices of the domain which map to arcs in the split tree which are connected to local maxima. We will now extract these regions.

Click on the top center view to activate it. Now, in the pipeline browser, select the Segmentation output of the first TTK Merge and Contour Tree (FTM) filter. Now, apply the Threshold filter, in order to only show these vertices that have a RegionType value of 1. This will extract all vertices mapping to arcs connected to local maxima. Change the display properties of these vertices to color them by the field SegmentationId (you can edit the color map by clicking on the Edit button). Trigger their visualization in the top left view, with the same coloring scheme.
You should now be visualizing something like this:
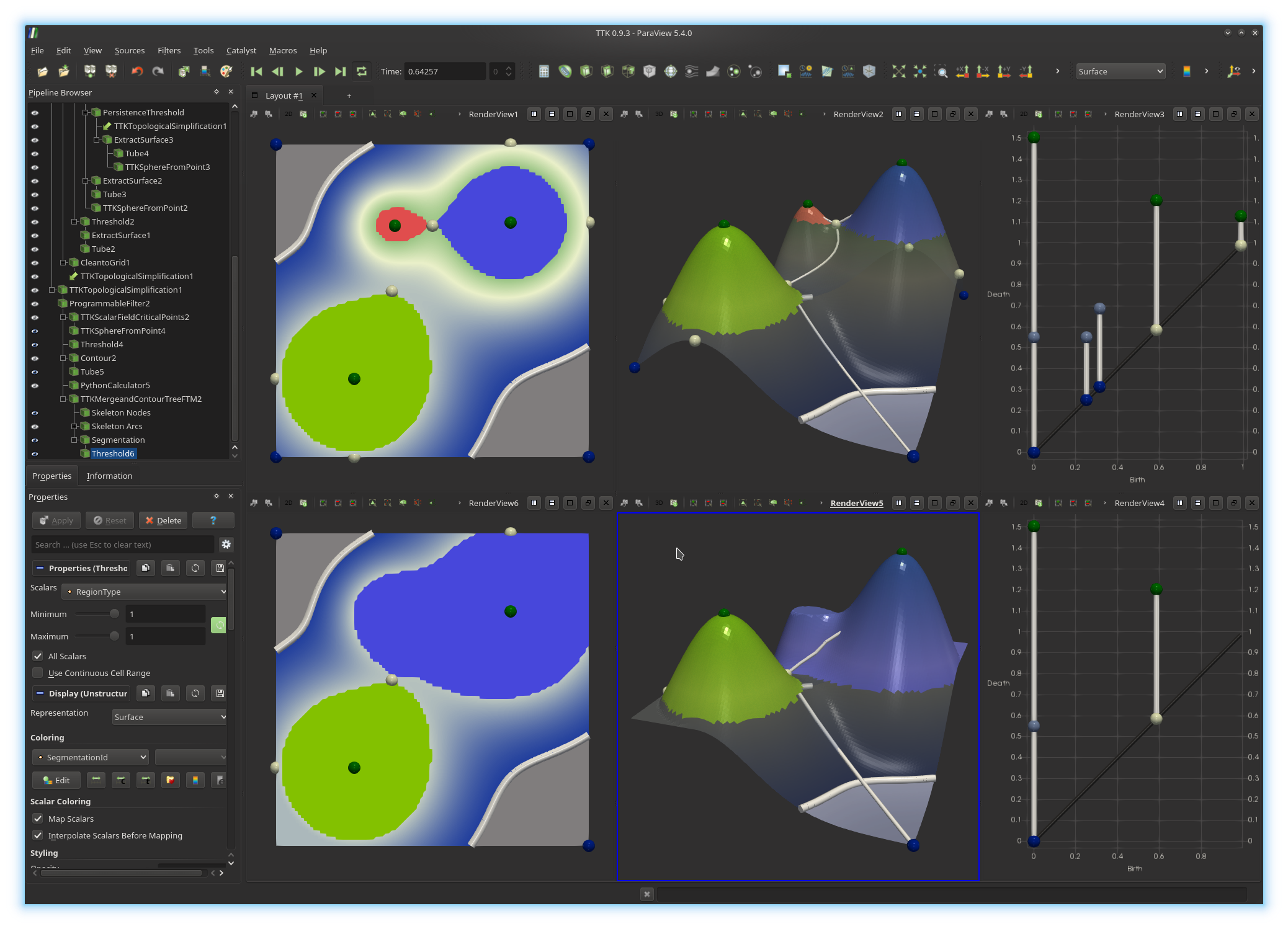
Now, go ahead and do the same thing for the simplified data in the bottom views.
If you managed to get a visualization similar to the above screenshot, congratulations!
You've just extracted the geometry of the two highest mountains of your terrain (bottom views). You can now play with the persistence threshold (beginning of exercise 7) to explore the hierarchy of your data segmentation.

6. Topological data segmentation in Python

We will now implement a similar analysis pipeline in Python, thanks to ParaView Python export capabilities.

Exercise 11

First, in your pipeline browser, select the output of your first Programmable Filter (corresponding to the first, non-simplified 3D terrain). Next, save this data to disk with the menu File, Save Data... (select the vtu file extension). You can now close ParaView.

Re-open now ParaView and load the file you have just saved. Split the current view horizontally and compute and display the persistence diagram of your data in this new view.

Now threshold your diagram to remove the diagonal and threshold again to remove low persistence pairs (see exercise 7). Next, activate the left view by clicking in it and select your 3D terrain in the pipeline browser and call the TTK TopologicalSimplification filter on it, using as constraints the persistent pairs you selected previously from the persistence diagram (see exercise 7).

Next, compute the split tree of the simplified data (see exercise 9, do not forget to check the box Use Input Offset Scalar Field). Finally, threshold the Segmentation output of the split tree, to only visualize vertices with a RegionType value of 1.
Update: as of version 0.9.6, there is no need to check the box UseInputOffsetField. Input offsets are now automatically retrieved from the data, if present. To force the usage of a specific field as vertex offset (advanced usage), check the box ForceInputOffsetField.

At this point, you should be visualizing something like this:
We will now convert this simple analysis pipeline into a Python script. For this, enter the menu File, Save state... and choose the Python state file type and save your file with the name pipeline.py.

We will now turn the generated Python script into an independently executable program.
This script relies on the Python layer of TTK and ParaView. It should be interpreted with pvpython, which wraps around the traditional Python interpretor, in order to set the required environment variables properly. To automatically run the script with the right interpretor, we will add the following line at the very top of the generated script:

#!/usr/bin/env pvpython

Next, we will make the script executable by setting its execution bit, by entering the following command (omit the $ character):

$ chmod +x pipeline.py

Your Python program can now be run by simply entering the following command (omit the $ character):

$ ./pipeline.py

By default, this program loads the input terrain, simplify the data, segment the mountains with the split tree and simply exits. We will now modify this script to store to disk the segmentation of the highest mountains.

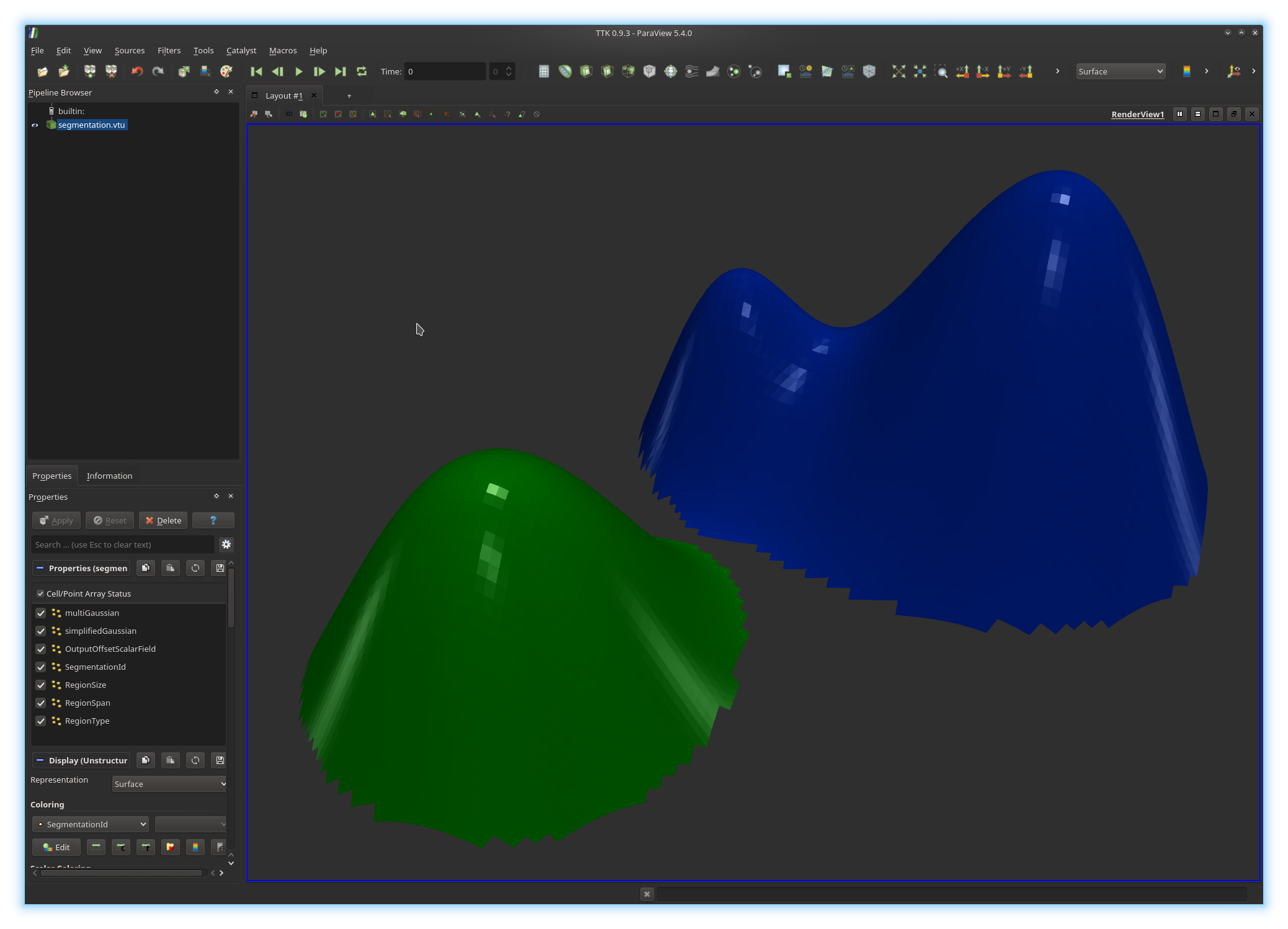
For this, open the script with a text editor and identify the part of the script which thresholds the segmentation according to the RegionType field. After this paragraph, add a Python instruction to save the Threshold object to disk, with the function SaveData(), which takes as a first argument a filename (for example segmentation.vtu) and as a second argument a pipeline object (here the instance of Threshold object). Save your file and execute your script. It should have written to disk a file named segmentation.vtu. Open it in ParaView. You should be visualizing something like this:
Note that other file formats are supported. Modify your script to save the segmentation into the file segmentation.csv instead of segmentation.vtu and run your script again. It should have produced a plain ASCII file storing the segmentation, which can be opened and parsed with any other software.

Exercise 12

Note that, in our Python script, the instructions located after the saving of the segmentation deal with rendering parameters. Thus, these can be removed in our context since we are using the script in batch mode. Other instructions related to render views can also be removed for the same reason.
Remove all the Python instructions that are not strictly necessary for the computation of the output segmentation. At this point, your script should have less than 25 instructions and should therefore be much easier to read.

Exercise 13

Now edit your Python script in order to read the persistence threshold with which the data should be simplified from the command line, as an argument of your Python script.

7. Topological segmentation of medical data

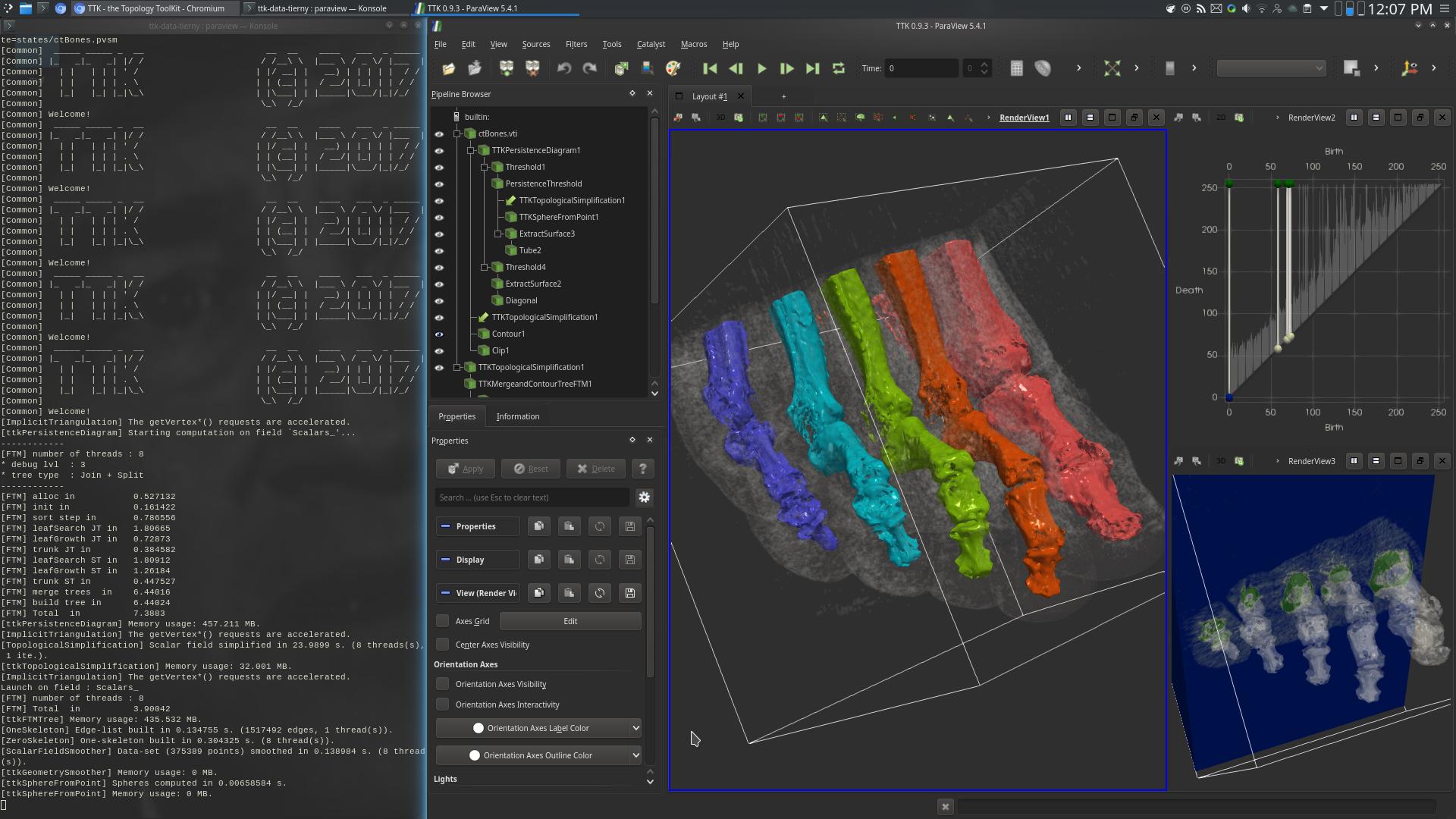
We will now apply our topological data analysis pipeline to some real-life medical data.
For this open with ParaView the following data set:

~/ttk/ttk-data-0.9.3/ctBones.vti

Now, deploy the topological data analysis pipeline we designed in this tutorial, in order to segment the 5 highest mountains of this CT scan:
   ·  Computation of the persistence diagram of the data;
   ·  Selection of the 5 most persistent pairs;
   ·  Topological simplification of the data according to the persistence selection;
   ·  Computation of the split tree of the simplified data;
   ·  Segmentation of the regions mapping to branches of the split tree connected to maxima;

If you got it right, your pipeline should precisely isolate the bones of the foot and you should be visualizing something like this:
If so, congratulations, you've just managed to segment medical data thanks to topological data analysis!