Persistence Clustering 0

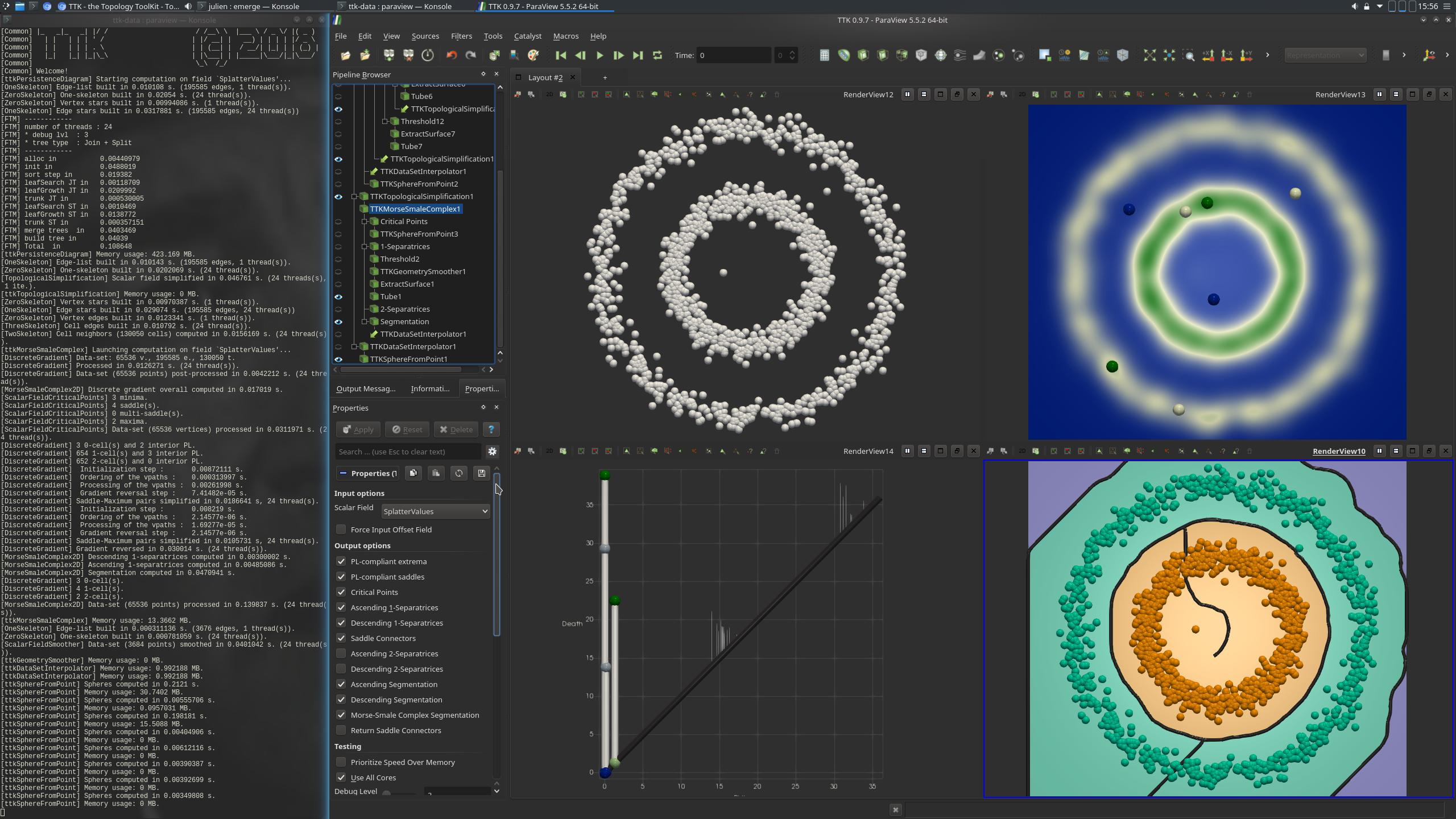
Pipeline description

This example performs a persistence driven clustering of a 2D toy data set, taken from the scikit-learn examples. Please check out the Karhunen-Love Digits 64-Dimensions example for an application of this pipeline to a real-life, high-dimensional, data set.

The pipeline starts by estimating the density of the input point cloud with a Gaussian kernel, by the GaussianResampling filter, coupled with the Slice filter (to restrict the estimation to a 2D plane).

Next, the PersistenceDiagram of the density field is computed and only the 2 most persistent density maxima are selected (corresponding to the desired 2 output clusters, bottom left view in the above screenshot).

Next, the simplified persistence diagram is used as a constraint for the TopologicalSimplification of the density field (top right view, above screenshot). The simplified density field then contains only 2 maxima and it is used as an input to the Morse-Smale complex computation, for the separation of the 2D space into the output clusters (background color in the bottom right view, above screenshot).

Finally, the cluster identifier of each input point is given by the identifier of the corresponding ascending manifold of the Morse-Smale complex (AscendingManifold), with the ResampleWithDataset filter.

ParaView

To reproduce the above screenshot, go to your ttk-data directory and enter the following command:

paraview states/persistenceClustering0.pvsm

Python code

#!/usr/bin/env python

from paraview.simple import *

# create a new 'CSV Reader'
clustering0csv = CSVReader(FileName=["clustering0.csv"])

# create a new 'Table To Points'
tableToPoints1 = TableToPoints(Input=clustering0csv)
tableToPoints1.XColumn = "X"
tableToPoints1.YColumn = "Y"
tableToPoints1.a2DPoints = 1
tableToPoints1.KeepAllDataArrays = 1

# create a new 'Gaussian Resampling'
gaussianResampling1 = GaussianResampling(Input=tableToPoints1)
gaussianResampling1.ResampleField = ["POINTS", "ignore arrays"]
gaussianResampling1.ResamplingGrid = [256, 256, 3]
gaussianResampling1.SplatAccumulationMode = "Sum"

# create a new 'Slice'
slice1 = Slice(Input=gaussianResampling1)
slice1.SliceType = "Plane"

# init the 'Plane' selected for 'SliceType'
slice1.SliceType.Normal = [0.0, 0.0, 1.0]

# create a new 'TTK PersistenceDiagram'
tTKPersistenceDiagram1 = TTKPersistenceDiagram(Input=slice1)
tTKPersistenceDiagram1.ScalarField = ["POINTS", "SplatterValues"]
tTKPersistenceDiagram1.IgnoreBoundary = False

# create a new 'Threshold'
persistenceThreshold0 = Threshold(Input=tTKPersistenceDiagram1)
persistenceThreshold0.Scalars = ["CELLS", "Persistence"]
persistenceThreshold0.ThresholdMethod = "Between"
persistenceThreshold0.LowerThreshold = 10.0
persistenceThreshold0.UpperThreshold = 999999999

# create a new 'TTK TopologicalSimplification'
tTKTopologicalSimplification1 = TTKTopologicalSimplification(
    Domain=slice1, Constraints=persistenceThreshold0
)
tTKTopologicalSimplification1.ScalarField = ["POINTS", "SplatterValues"]

# create a new 'TTK MorseSmaleComplex'
tTKMorseSmaleComplex1 = TTKMorseSmaleComplex(Input=tTKTopologicalSimplification1)
tTKMorseSmaleComplex1.ScalarField = ["POINTS", "SplatterValues"]

# create a new 'Resample With Dataset'
resampleWithDataset1 = ResampleWithDataset(
    SourceDataArrays=OutputPort(tTKMorseSmaleComplex1, 3),
    DestinationMesh=tableToPoints1,
)
resampleWithDataset1.CellLocator = "Static Cell Locator"

SaveData("OutputClustering.csv", resampleWithDataset1)

To run the above Python script, go to your ttk-data directory and enter the following command:

pvpython python/persistenceClustering0.py

Inputs

• clustering0.csv: a 2D point cloud taken from the scikit-learn examples.

Outputs

• OutputClustering.csv: the output clustering of the input point cloud (output cluster identifier: AscendingManifold column)

C++/Python API

Morse-Smale complex

PersistenceDiagram

TopologicalSimplification